AP Statistics
Sections: 1.|  Inference for a Population Proportion  2.| Comparing Two Proportions

   Inference for a Population Proportion

The population mean and the sample mean are not the only parameter and statistic used by statisticians.  Proportion or percent are often used to describe a situation.  Unemployment, the rate of inflation, the strength of a medication, the percent of defects, etc. are examples of situations that use proportions.

Similar to the sampling distribution of sample means, the sampling distribution of sample proportions follows the Central Limit Theorem.  This distribution is defined as

N(po, ). 

Plotting sample proportions from the same population will produce a Normal distribution with mean po (mean of the sample proportions will approach the population mean po) and standard error

 .

The confidence level for po is found by the formula

Confidence Interval for a Population Proportion 

                         where:   po is the population proportion
                                      the sample proportion is the point estimate.
                                      z is the score (confidence level)
                                      n is the sample size
 

Example:

The US Labor Bureau interviewed 1,200 people.  It was found that 41 of those people surveyed were unemployed.   Find a 95% confidence interval for the population unemployment rate.
Solution
Identifying the variables, x = 41,  n = 1,200  samplep.gif (870 bytes) = 41/1200 = 0.034, and z = +1.96 . 

Substituting into the formula produces

Thus a 95% confidence interval for the population unemployment rate is 0.024 < po< 0.044.

Example:

Find a 99% confidence interval for the population unemployment rate using the information from Example 1.
Solution
Identifying the variables, n = 1,200  samplep.gif (870 bytes) = 0.034, and z = +2.575 . 

Substituting into the formula produces

Thus a 99% confidence interval for the population unemployment rate is 0.021 < po < 0.047.

Sample Size
Manipulating the confidence level and sample size changes the confidence interval. There is a minimum sample size required for a desired confidence level and an acceptable error.  The formulas are

Sample Size for the Confidence Interval for the Population Proportion

         When the estimate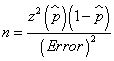 samplep.gif (870 bytes) is known

         When the estimate samplep.gif (870 bytes) is unknown

        where:  z is the standard score for the confidence level
                     samplep.gif (870 bytes)is the sample proportion
                     Error is the allowable error
 

Example:

What is the minimum number of parts that must be tested to find a 95 % confidence interval for the population defect rate?  Last month's defect rate was 2.1% and the allowable error is + 1%.
Solution
Identifying the variables:  samplep.gif (870 bytes) = 0.021,  Error = 0.01  and z = 1.95.  Substituting into the formula for sample size=

Thus the company needs to check 782 parts. (Note since you cannot test a fraction of a customer, the sample size is bumped up to the next whole number for any fraction.)

Example: 

What is the minimum number of parts that must be tested to find a 95 % confidence interval for the population defect rate?   This is a new procedure and thus no sample proportion exists.  The allowable error is + 1%.
Solution
Identifying the variables:  samplep.gif (870 bytes) = ?,  Error = 0.01  and z = 1.96.  Substituting into the formula for sample size

                    =         

Thus the company needs to check 9,604 parts.

  
Try Self Check 16

Hypothesis testing for a single proportion

Similar to testing the validity of a claim about  a population mean, µ, when σ, the population standard deviation, is known or unknown.  Claims made about the population proportion, po, can also be tested for their validity.

In this section all problems will involve samples that satisfy the following prerequisites for testing a claim about a proportion.

Assumptions for Testing a Claim About a Proportion

   1.  The data is a simple random sample taken from the population.
   2.  The population is at least 10 times at large as the sample.
   3.  Both np and n(1 - p) are at least 10. 
        where: p is the proportion used in the hypothesis statements

The test statistic "z" is used in this case.  The formula for the test statistic is

Test Statistic for Proportions

    where: samplep.gif (870 bytes) is the sample proportion
                 po is the proportion used in the hypothesis statements
                 n is the sample size
 

Example:

The percent of people who voted to increase their taxes for the fire protection district was 42% in the last referendum.  A recent survey of 300 residents produced 130 people who would vote favorably to increase their taxes for the fire department.  At a 0.01 level of significance has the proportion of people in favor of the tax referendum increased since the last referendum?
Solution:
The claim is about a population proportion.  Use the z-score to test the validity of this claim.  The data values are:
                                         a. Population population (po) = 42% = 0.42
                                         b. Sample proportion (samplep.gif (870 bytes)) = 130 / 300 = 0.4333
                                         c. Sample size (n) = 300
                                         d. Level of significance (α) = 0.01

The claim, "the proportion has increased" translates into po > 0.42. 
   Ha: po > 0.42 claim
The Null Hypothesis, H0, and the diagram are:
   H0: po = 0.42 and

normgrtn.gif (2960 bytes)

The corresponding diagram has only one "Reject H0" region, so the 0.01 level of significance is assigned to this region. 

normgrt1.gif (3056 bytes)

Check assumptions: We have to assume the population is 10 times larger than the sample even though is it not stated and it is a SRS. np = (300)(0.4333) = 130 and nq = (300)(0.5666) = 170. Since both are greater than 10 it is safe to use the normal approximation. Similar to calculating a confidence interval for a population proportion, the "z-test" is chosen as the test statistic.

In this problem, the p-value is 0.3199.  Starting on the side of the rejection region move into the Normal curve a distance of 0.3199.

hypotpx1.gif (3354 bytes)

Since the p-value did cross the 0.01 line, separating the "Reject H0" region from the "Fail to Reject H0" region, the decision is to "Fail to Reject the Null Hypothesis, H0".

Conclusion

In conclusion, the Null Hypothesis, H0, is not rejected and the data appears to support the claim. The proportion does appear to have remained the same since the last referendum.
 

Example: 

The percent of people who voted to increase their taxes for the fire protection district was 42% in the last referendum.  A recent survey of 300 residents produced 130 people who would vote favorably to increase their taxes for the fire department.  At a 0.01 level of significance has the proportion of people in favor of the tax referendum remained the same since the last referendum?
Solution:
The claim is about a population proportion.  Use the z-score to test the validity of this claim.  The data values are:
                            a. Population population (p) = 42% = 0.42
                            b. Sample proportion (samplep.gif (870 bytes)) = 130 / 300 = 0.4333
                            c. Sample size (n) = 300
                            d. Level of significance (α) = 0.01

Translate the claim, "the proportion remained the same" translates into p = 0.42.  .
     H0: po = 0.42 claim
The Alternate Hypothesis, Ha, and the diagram are:
     Ha: po notequal.gif (844 bytes)0.42 and

normleq.gif (3085 bytes)

The corresponding diagram has two "Reject H0" regions, so the 0.01 level of significance is divided in half and assigned to each region.  (Note that because of symmetry, the size of each rejection region is α / 2.)

nrmleq1.gif (3331 bytes)

Check assumptions: We have to assume the population is 10 times larger than the sample even though is it not stated and it is a SRS. np = (300)(0.4333) = 130 and nq = (300)(0.5666) = 170. Since both are greater than 10 it is safe to use the normal approximation. Similar to calculating a confidence interval for a population proportion, the "z-test" is chosen as the test statistic. Similar to calculating a confidence interval for a population proportion, the "z-test" is chosen as the test statistic.

In this problem, the p-value is 0.6399.  Since the Null Hypothesis is   H0: po = 0.42 the p value is 0.6399/2 = 0.31995.   Starting on either side of the rejection region move into the Normal curve a distance of 0.31995.

hypotpx2.gif (3617 bytes)

Since the p-value did cross the 0.01 line, separating the "Reject H0" region from the "Fail to Reject H0" region, the decision is to "Fail to Reject the Null Hypothesis, H0".

Conclusion

In conclusion, the Null Hypothesis, H0, is not rejected and the data appears to support the claim. The proportion does appear to have remained the same since the last referendum.
 

Try Self Check 17

Proceed to Multiple Choice 8

Proceed to Statistics Assignment 10: Working with a Single Proportion
© 2004 Aventa Learning. All rights reserved.