Lesson 5.01 Distance and Displacement

Motion

Motion happens all the time and has many different aspects to it, which we will cover in this lesson and the following lessons in this unit. Think about a runner who's running a race. There are multiple aspects to the runner's overall motion, including:

• the runner's speed
• how fast the runner is accelerating
• the distance the runner travels.

All of these are important aspects of motion.

Frames of Reference

Let's think about someone watching the race. If you were watching a runner during a race, how would you know that the runner was in motion? Reveal Answer

The frame of reference is a system for specifying the precise location of objects in space and time. Objects in motion can move at different speeds and different directions. In this lesson you will learn how to analyze the motion of objects. When calculating the motion of an object, you must first choose a frame of reference.

In the example of the runner in a race, a good frame of reference would be the starting line of the track. That is an easy place to measure the distance or how far and fast the runner has traveled.

Think about the question: How far have you traveled today?

• It's hard to answer that question precisely!
• It could mean how far you have driven or how many steps you have taken.
• Without a specific frame or reference, measuring motion (including aspects of motion such as speed and distance) becomes more difficult.

To learn more about frames of reference, review the Relative Motion interactive.

Why is an understanding of frames of reference important? Reveal Answer

→ »

Motion Dimensions

Besides needing a frame of reference to properly measure and describe motion, you should also recognize before moving further in this unit that motion can occur in both one dimension and in two dimensions. Let's talk about what that means.

One-Dimensional Motion

Think back to the runner running along the track — let's say he's running the 100 meter dash. This runner's motion is considered one-dimensional because the runner is running along a straight line.

In one-dimensional motion, an object moves in a straight line. The object can move either forward or backward on the line.

• An object moving forward (usually considered to the right) is considered to have positive movement.
• An object moving backwards (usually to the left) is considered to have negative movement.

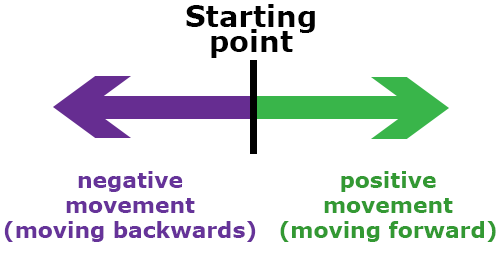
One-dimensional positive movement is generally shown moving to the right and one-dimensional negative movement can be thought of as moving left.

Two-Dimensional Motion

Now, picture a quarterback throwing a football downfield to a receiver. The motion of the football is considered two-dimensional. Why? Well, the football travels in two directions at the same time.

• The football is moving horizontally down the field toward the receiver.
• At the same time, the football is moving vertically in the air (to keep it from being blocked by the lineman).
• This makes the shape of the motion of football look similar to an arch — sometimes called a parabola.

Which is Which?

We will discuss these types of motion more when we move to graphing motion. Look at the pictures below and try to identify which represents one-dimensional motion motion in a straight line and which represents two-dimensional motion motion both horizontally and vertically .

Rollover each image to check your answers!

« → »

Distance

As you know, there are many different aspects of motion. For this lesson, we are going to focus on two aspects, and we will continue to add to these aspects as we move through the unit. In this lesson we will focus on distance and displacement.

Distance

Distance is the total length traveled. In measuring distance, it does not really matter what direction the travel is in, just the total amount of distance covered.

For example, Forrest:

• Walks 12 meters
• Turns left and walks 10 meters
• Turns right and walks 4 meters
• Then stops.

To find the total distance Forest traveled, we just add up all the different lengths he walked:

12 m + 10 m + 4 m = 26 meters

The total distance total length traveled is 26 m.

Now you try one. Sally:

• Walks 16 m east
• Turns and walks 3 m west
• Then turns again and walks 5 m south

What is the total distance Sally walked? Check Your Answer

« ← → »

Displacement

Displacement is similar to distance but with one very important difference — displacement takes into account the direction of the motion.

• Displacement is the change in position of an object.
• This means that displacement can be either positive or negative, depending on which direction the object moves.
• Displacement is not always equal to distance.

Think about this example:

• I leave my house and walk around my block, which is a total of 35 m.
• At the end I return to the exact point (my house) that I began.
• What was my distance total length traveled and my displacement change in position ?

Well, figuring out the distance is easy. I walked 35 m around the block so my distance traveled is 35 m.

Displacement may not be quite as easy to see. Remember, displacement is change in position. In the question, I began and ended at the same position (my house) so my displacement is 0 m.

The formula for finding displacement is:

Change in position = final position — initial position

Δx = x_f - x_i

In this formula:

• Δ = The change in position (the delta symbol, or Δ, means “change in”)
• x_f = final position
• x_i = initial position

Displacement can be either positive or negative and is not always the distance traveled. The initial position(x_i) and final position (x_f) are the start and the end of any interval you choose. The direction can be indicated by a plus or minus sign.

When the displacement is in the same direction, you add like (or same) units. For example, if someone travels 5 m east and then 4 meters east, his displacement would be 9 m (5 m east + 4 m east = 9 m east). In this case, because the different parts of the motion were both in the same direction (east), we were able to just add them together — which also means the displacement was the same as the distance.

When the motion is not all in the same direction, you must compare your values or your directions. If the motion is in opposite directions, you will need to subtract. For example, a girl on a bicycle:

• Rides 9 m east
• Turns around
• Then rides 3 m west

What is her displacement?

Well, if she went 9 meters east but then came back west for 3 meters, she really only changed position by 6 meters. Therefore, her displacement is 6 m east (9 m east - 3 m west = 6 m east).

Visit the Physics Classroom to learn more about distance and displacement. Be sure to read the entire page and complete the two Check Your Understanding questions at the bottom.

« ← »

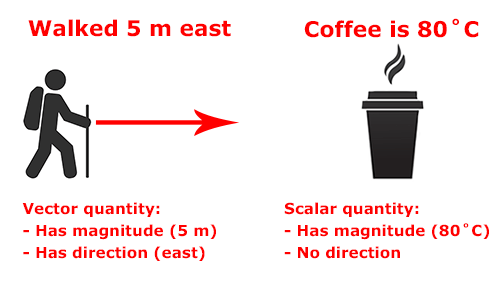
Vector

Motion is often described by the use of vectors. A vector quantity is a value that has both a magnitude (think number of value) and a direction (could be measured by a cardinal direction the 4 main points on a compass: north, south, east, and west or a degree sign).

• Sometimes, vector quantities are drawn on graphs using arrows.
• The size of the arrow represents the magnitude while the arrow itself points in the correct direction.

Scalar

If something is not a vector quantity, we usually refer to it as scalar. A scalar quantity has a magnitude (measurement or value) but no direction. For example, if I say the temperature of a cup of coffee is 80°C, that is a scalar quantity. It has no direction.

Watch the video Physics Fundamentals: Introduction to Vectors to the 20:18 minute mark. Use the video to complete 5.01 Distance and Displacement Note-taking Guide. Login information.

To complete this assignment, you will need a protractor. See the Task page for submission information.

« ←