4.08 Graphs of Other Trig Functions

Try It

Graphs of Other Trig Functions Practice

Practice 1: Tangent/Cotangent

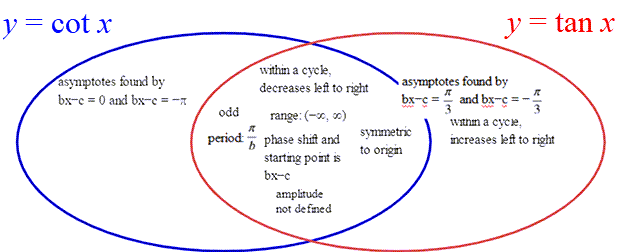
Drag each description to its appropriate place on the Venn diagram.

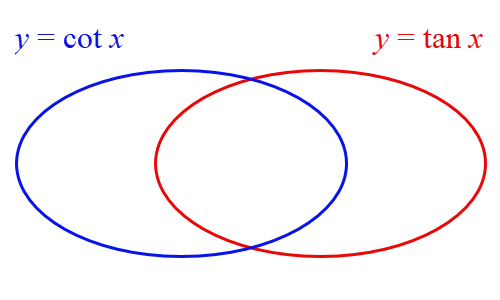
Definitions:

1. asymptotes found by bx−c = 0 and bx−c =

A. y = a × cot(bx − c)

B. y = a × tan(bx − c)

C. Both y = a × cot(bx − c) AND y = a × cot(bx − c)

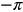
2. within a cycle, decreases left to right

A. y = a × cot(bx − c)

B. y = a × tan(bx − c)

C. Both y = a × cot(bx − c) AND y = a × cot(bx − c)

3. range: (−∞, ∞)

A. y = a × cot(bx − c)

B. y = a × tan(bx − c)

C. Both y = a × cot(bx − c) AND y = a × cot(bx − c)

4. amplitude not defined

A. y = a × cot(bx − c)

B. y = a × tan(bx − c)

C. Both y = a × cot(bx − c) AND y = a × cot(bx − c)

5. odd

A. y = a × cot(bx − c)

B. y = a × tan(bx − c)

C. Both y = a × cot(bx − c) AND y = a × cot(bx − c)

6. 

A. y = a × cot(bx − c)

B. y = a × tan(bx − c)

C. Both y = a × cot(bx − c) AND y = a × cot(bx − c)

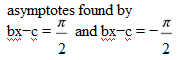
7. within a cycle, increases left to right

A. y = a × cot(bx − c)

B. y = a × tan(bx − c)

C. Both y = a × cot(bx − c) AND y = a × cot(bx − c)

8. phase shift and starting point is bx−c

A. y = a × cot(bx − c)

B. y = a × tan(bx − c)

C. Both y = a × cot(bx − c) AND y = a × cot(bx − c)

9. symmetric to origin

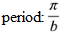
A. y = a × cot(bx − c)

B. y = a × tan(bx − c)

C. Both y = a × cot(bx − c) AND y = a × cot(bx − c)

10. 

A. y = a × cot(bx − c)

B. y = a × tan(bx − c)

C. Both y = a × cot(bx − c) AND y = a × cot(bx − c)

Answers:

1. A. y = a × cot(bx − c)
2. C. Both y = a × cot(bx − c) AND y = a × cot(bx − c)
3. C. Both y = a × cot(bx − c) AND y = a × cot(bx − c)
4. C. Both y = a × cot(bx − c) AND y = a × cot(bx − c)
5. C. Both y = a × cot(bx − c) AND y = a × cot(bx − c)
6. B. y = a × tan(bx − c)
7. B. y = a × tan(bx − c)
8. C. Both y = a × cot(bx − c) AND y = a × cot(bx − c)
9. C. Both y = a × cot(bx − c) AND y = a × cot(bx − c)
10. C. Both y = a × cot(bx − c) AND y = a × cot(bx − c)

Practice 2: Secant/Cosecant

Drag each description to its appropriate place on the Venn diagram.

Definitions:

1. asymptotes found by bx − c = 0 and bx−c =

A. y = a × csc(bx − c)

B. y = a × sec(bx − c)

C. Both y = a × csc(bx − c) AND y = a × sec(bx − c)

2. no x−intercepts

A. y = a × csc(bx − c)

B. y = a × sec(bx − c)

C. Both y = a × csc(bx − c) AND y = a × sec(bx − c)

3. symmetric to origin

A. y = a × csc(bx − c)

B. y = a × sec(bx − c)

C. Both y = a × csc(bx − c) AND y = a × sec(bx − c)

4. 

A. y = a × csc(bx − c)

B. y = a × sec(bx − c)

C. Both y = a × csc(bx − c) AND y = a × sec(bx − c)

5. 

A. y = a × csc(bx − c)

B. y = a × sec(bx − c)

C. Both y = a × csc(bx − c) AND y = a × sec(bx − c)

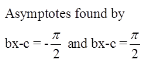
6. odd

A. y = a × csc(bx − c)

B. y = a × sec(bx − c)

C. Both y = a × csc(bx − c) AND y = a × sec(bx − c)

7. range: (−∞, −1), (1, ∞)

A. y = a × csc(bx − c)

B. y = a × sec(bx − c)

C. Both y = a × csc(bx − c) AND y = a × sec(bx − c)

8. even

A. y = a × csc(bx − c)

B. y = a × sec(bx − c)

C. Both y = a × csc(bx − c) AND y = a × sec(bx − c)

9. phase shift and starting point is bx−c

A. y = a × csc(bx − c)

B. y = a × sec(bx − c)

C. Both y = a × csc(bx − c) AND y = a × sec(bx − c)

10. amplitude not defined

A. y = a × csc(bx − c)

B. y = a × sec(bx − c)

C. Both y = a × csc(bx − c) AND y = a × sec(bx − c)

11. symmetric to y−axis

A. y = a × csc(bx − c)

B. y = a × sec(bx − c)

C. Both y = a × csc(bx − c) AND y = a × sec(bx − c)

Answers:

1. A. y = a × csc(bx − c)
2. C. Both y = a × csc(bx − c) AND y = a × sec(bx − c)
3. A. y = a × csc(bx − c)
4. C. Both y = a × csc(bx − c) AND y = a × sec(bx − c)
5. B. y = a × sec(bx − c)
6. A. y = a × csc(bx − c)
7. C. Both y = a × csc(bx − c) AND y = a × sec(bx − c)
8. B. y = a × sec(bx − c)
9. C. Both y = a × csc(bx − c) AND y = a × sec(bx − c)
10. C. Both y = a × csc(bx − c) AND y = a × sec(bx − c)
11. B. y = a × sec(bx − c)

Practice 3: Sketching a Graph

Find the following for y = tan(2x − 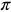), then sketch the graph.

Phase shift: bx − c = 0

• _____ (Fill in the blank) x − 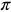= 0


• Answer: 2 x − 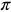= 0


• 2x =
• 
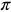
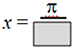
• Answer:
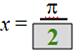
• Period: period =
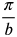
• period =


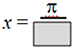
• Answer:
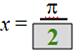
• Two consecutive vertical asymptotes:
• bx − c = −
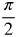
• bx − c =
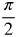
• _____ (Fill in the blank)x − = −
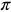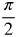
• _____ (Fill in the blank)x − =
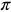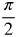
• Answer:
• 2x − = −
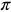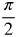
• 2x − =
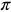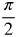
• _____ (Fill in the blank)x = − +
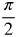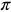
• _____ (Fill in the blank)x = +
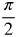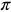
• Answer:
• 2x = − +
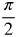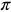
• 2x = +
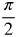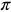
• x =
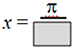
• x =


• Answer:
• x =


• 


• 

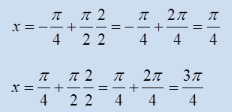
Draw the graph on the next slide.

Practice 3: Sketching a Graph

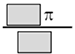
On your own paper, using the information below, sketch the graph of

• y = tan(2x − )
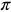• phase shift: x =
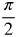
• period =
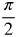
• vertical asymptotes: 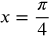and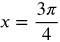
• Draw the vertical asymptotes
• Find the x−intercepts, the midpoints between the asymptotes
• Sketch the cycles
• Click Reveal to check your graph

• 

• Answer:

• 

• You can also check your graph on the calculator.
• Click Mode, then Radian.
• Now click Y= and enter Y1= tan(2x − 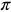) . Then select Zoom 7: ZTrig .