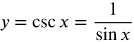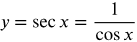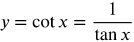Learn
Graphs of Other Trig Functions
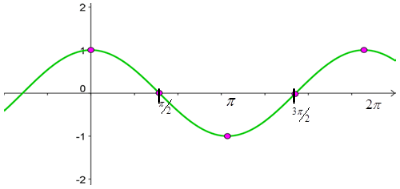
Now that you can graph the cosine and sine functions, we will look at the other trigonometric functions. Let’s start with tangent.
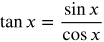so the tangent is undefined when cos x = 0
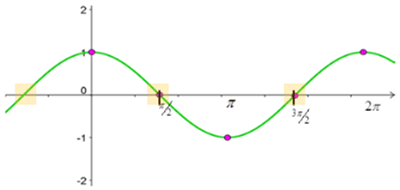
cos x = 0 at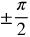 
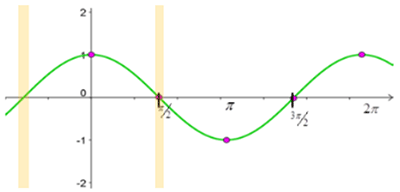Let’s look at values between these two points.
Graphing Tangent Functions
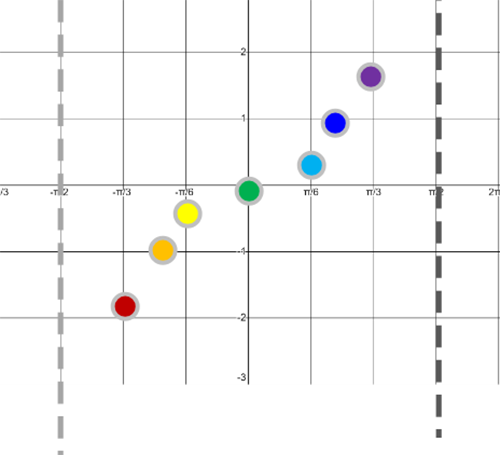
Use your calculator to fill in this chart. If an answer is not possible, the answer will be “undefined.”
| x |  |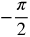
−1.57 | −1.5 | −1 | 0 | 1 | 1.5 | 1.57 |  |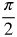
| tan x |
| x | |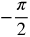
−1.57 | −1.5 | −1 | 0 | 1 | 1.5 | 1.57 | |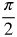
| tan x | und | −1255 | −14 | −1.6 | 0 | 1.6 | 14 | 1255 | und |
As x approaches 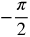the tan x approaches −∞
As x approaches 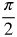the tan x approaches ∞
This means the tan x has vertical asymptotes at 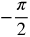and
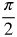
Graphing Tangent Functions
Plot some points from the chart by dragging each dot to its location on the graph. If the point is too large to fit on the graph, drop it off the appropriate end. Drag the asymptotes to the appropriate places as well. On your calculator graph y=tan (x) to see the general shape of the function.
.
Answer:
Graphing Tangent Functions
Now that we have the tangent function graphed, let’s look at its characteristics.
Amplitude: not defined
Range: (−∞, ∞)
Tangent function is odd tan(−x) = −tan(x)
Tangent function is symmetric to the origin
Vertical asymptotes at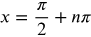 
Domain: all real numbers except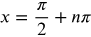
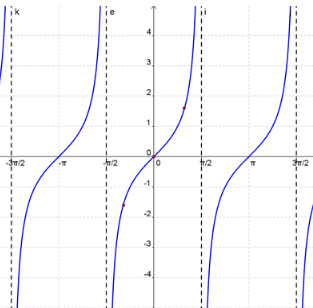
Parent Tangent Function
Let's summarize what we know about the parent function y = tan x:
Tangent is an odd function (that doesn't mean that its phase- or vertically-shifted counterpart will be).
Tangent is always increasing between any two vertical asymptotes.
Vertical asymptotes occur at +nπ, where n is any integer.
The domain of tangent can also be expressed as all real numbers except for odd integer multiples of .
The range is all real numbers. y = tan x is π-periodic, unlike sine/cosecant and cosine/secant.
The x-intercepts of the parent function are at integer multiples of π, aka πn, where n is any integer.
Standard Form of the Tangent Function
Here’s the standard form for the function of the tangent graph:
y = a tan (bx − c) + d
- Amplitude is not defined.
- Even though amplitude is not defined, the graph can still be vertically stretched/shrunk by the a parameter.
- Range: (−∞, ∞)
- Two consecutive vertical asymptotes can be found by solving
- period =
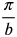
- Phase shift and starting point is bx − c = 0
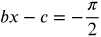and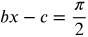 
To find out more, use Explore! Tangents.
Sketch a Graph of the Tangent Function
Open Sketch a Graph of the Tangent Function in a new tab
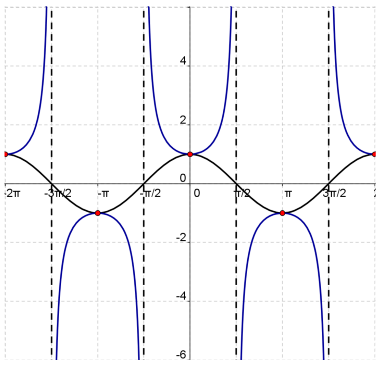
Graph of the Cotangent Function
Now that you have learned about the tangent function, let’s look at the cotangent function. The cotangent function is similar to the tangent function.
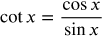so the cotangent is undefined when sin x = 0
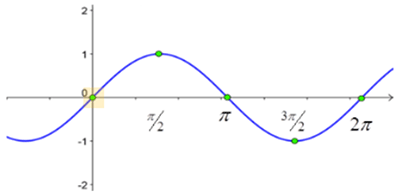
sin x = 0 at x = 0
, x =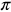 
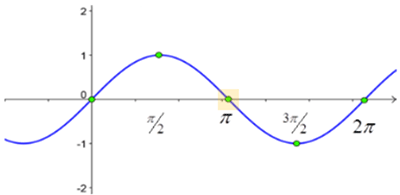, and x = 2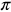
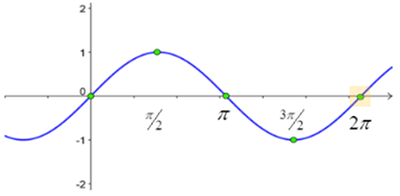
Below is the graph of y = sinx
Graph of the Cotangent Function
Now that you have learned about the tangent function, let’s look at the cotangent function. The cotangent function is similar to the tangent function.
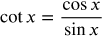so the cotangent is undefined when sin x = 0
sin x = 0 at x = 0, x = 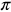, and x = 2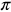
This means cot x has vertical asymptotes at 0, 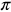, and 2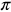
Vertical asymptotes occur at x = n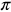
Domain: all real numbers except x = n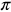
Graph of the Cotangent Function
The x-intercepts
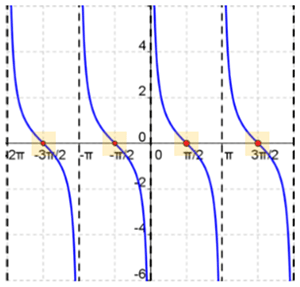are the midpoints between two consecutive vertical asymptotes.
On your calculator graph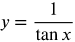 
to see the general shape of the function.
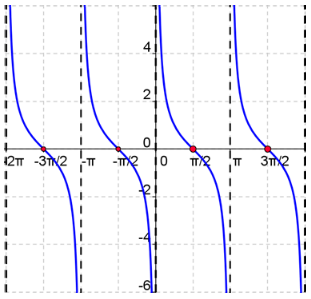
Parent Cotangent Function
Let's summarize what we know about the parent function y = cot x:
Cotangent is an odd function (that doesn't mean that its phase- or vertically-shifted counterpart will be).
Cotangent is always decreasing between any two vertical asymptotes.
Vertical asymptotes occur at all integer multiples of π.
The domain of cotangent can also be expressed as all real numbers except for integer multiples of π.
The range is all real numbers.
y = cot x is π-periodic, unlike sine/cosecant and cosine/secant.
The x-intercepts occur at +nπ, where n is any integer.
Standard Form of the Cotangent Function
Here’s the standard form for the function of the tangent graph:
y = a cot (bx − c) + d
- Amplitude is not defined.
- Even though amplitude is not defined, the graph can still be vertically stretched/shrunk by the a parameter.
- Range: (−∞, ∞) d is a vertical shift.
- period =
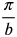
- Phase shift and starting point is bx − c = 0
To find out more, use Explore! Cotangents.
Graph the Function Cotangent
Open Graph the Function Cotangent in a new tab
Graphs of the Reciprocal Functions
The other two trigonometric functions, the cosecant and secant, are the reciprocals of the sine and cosine respectively.
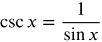The cosecant is undefined when sin x = 0
These points on the sine curve will be vertical asymptotes on the cosecant curve.
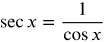The secant is undefined when cos x = 0
These points on the cosine curve will be vertical asymptotes on the secant curve.
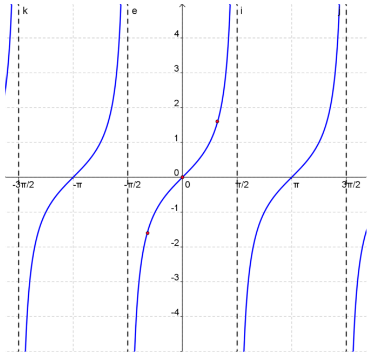
Graphing the Cosecant Function
Graph y = cosecant (x)
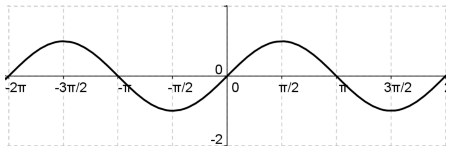
Because, we start by graphing y = sin x
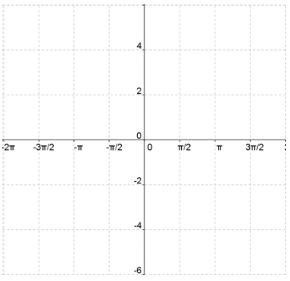
- Answer:
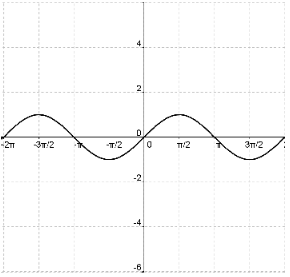
- The vertical asymptotes appear where sin x = 0. Draw these in by sketching an asymptote through each x–intercept.
- Find the reciprocal of the sin values to graph the cosecant.
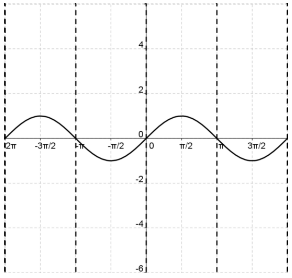
- Your final graph should look like this.
Parent Cosecant Function
The parent secant function is odd.
The domain is all real numbers, except integer multiples of π.
The range is (−∞, −1] ∪ [1, ∞).
There are no x-intercepts.
There are no y-intercepts.
Asymptotes occur at all integer multiples of π.
Standard Form of the Cosecant Function
Here’s the standard form for the function of the cosecant graph:
y = a csc (bx − c) + d
- A vertical or phase shift may result in the function no longer being odd.
- Amplitude is not defined.
- d is a vertical translation.
- The range is affected by a such that the range = (-∞, -a] ∪ [a, ∞).
- Two consecutive vertical asymptotes can be found by solving bx − c = 0 and bx − c = π
- period =
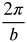
- Phase shift and starting point is bx − c = 0
To find out more, use Explore! Cosecants.
Sketch the Graphs of Cosecant Functions
Open Sketch the Graphs of Cosecant Functions in a new tab
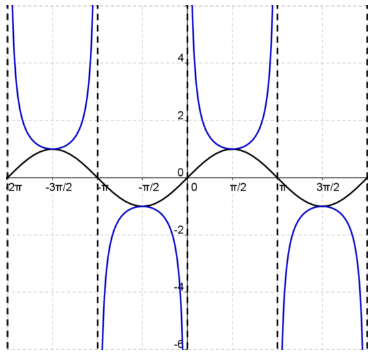
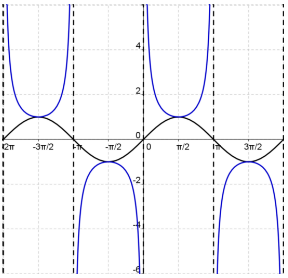
Graphing the Secant Function
Graph y = secant (x)
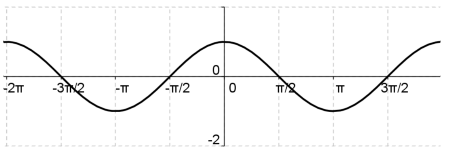
Because 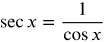, we start by graphing y = cos x
You will have vertical asymptotes where cos x = 0
Find the reciprocal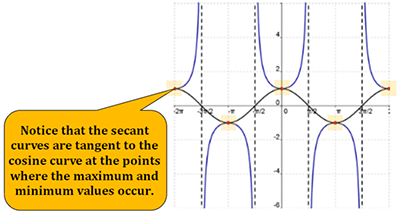 
of the cos values to graph the secant.
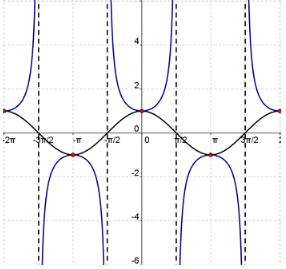
Parent Secant Function
Let's summarize what we know about the parent function y = sec x:
The parent secant function is even.
The domain is all real numbers, except at +π where n is an integer.
The range is (−∞, −1] ∪ [1, ∞).
There are no x-intercepts.
The y- intercept is (0, 1).
Asymptotes occur at odd integer multiples of .
Standard Form of the Secant Function
Here’s the standard form for the function of the secant graph:
y = a sec (bx − c) + d
- A phase shift may result in the function no longer being even.
- Amplitude is not defined.
- d is a vertical translation.
- The range is affected by a such that the range = (-∞, -a] ∪ [a, ∞).
- Two consecutive vertical asymptotes can be found by solving
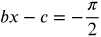and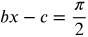
- There are no x–intercepts.
- period =
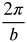
- Phase shift and starting point is bx − c = 0
To find out more, use Explore! Secants.
Sketch the Graphs of Secant Functions
Open Sketch the Graphs of Secant Functions in a new tab
Summarizing the Graphs of the Six Basic Trig Functions
Click on each tab to see the graph of that function.
- y = sin x
- y = cos x
- y = tan x
