Learn
Right Triangle Trigonometry
Consider a right triangle with one of the acute angles as the angle θ
The three sides are:
- Hypotenuse
- Side opposite the angle θ
- Side adjacent to the angle θ
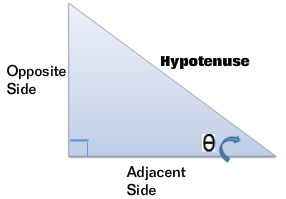
Right Triangle Trigonometry
The ratios of the lengths of these three sides are used to define the six trigonometric functions.


Abbreviations commonly used in right triangle trig: hypotenuse = hyp, opposite side = opp, adjacent side = adj
Finding the Trig Values
Find the exact values of the six trig functions for the angle θ
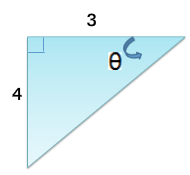
In order to find these trigonometric values, we need to know the lengths of all sides. We do not know the length of the hypotenuse, but can find it using the Pythagorean theorem.
Using the Pythagorean theorem, the length of the hypotenuse is:
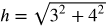
h = √25
h = 5
Finding the Trig Values
Find the exact values of the six trig functions for the angle θ
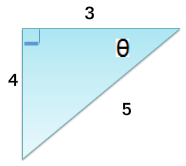
Now that we know the lengths of all sides of the triangle, we can solve the ratios by plugging in the values for the appropriate sides.
Trig Functions 1-3
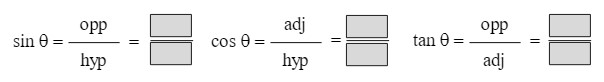
Answers:
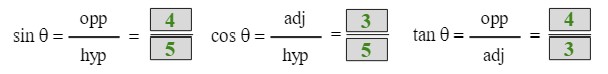
Trig Functions 4-6
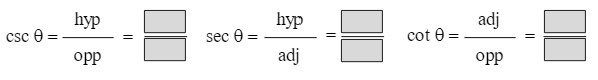
Answers:
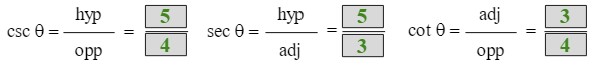
Find the exact values of the six trig functions for the angle θ. Review the solutions below.

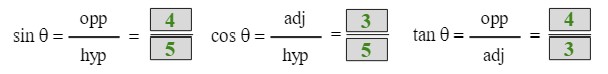
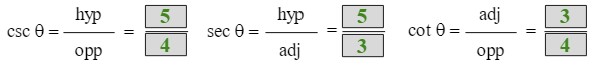
Evaluate Trigonometric Functions of the Acute Angles of a Right Triangle
Open Evaluate Trigonometric Functions of the Acute Angles of a Right Triangle in a new tab
Frequently Used Angles 1
The angles 30° or ![]() , 45° or
, 45° or ![]() , and 60° or
, and 60° or ![]() are used frequently in
trigonometry. It is necessary to learn their exact values.
are used frequently in
trigonometry. It is necessary to learn their exact values.
Construct a right triangle with one of the acute angles being 45° and the sides having a length of 1.
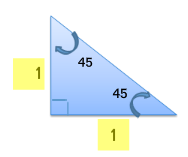
Using the Pythagorean theorem, the length of the hypotenuse is:
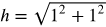
h = √2
The angles 30° or ![]() , 45° or
, 45° or ![]() , and 60° or
, and 60° or ![]() are used frequently in
trigonometry. It is necessary to learn their exact values.
are used frequently in
trigonometry. It is necessary to learn their exact values.
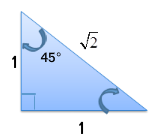
Now that we know the lengths of all sides of the triangle, we can solve the ratios by plugging in the values for the appropriate sides.
Trig Functions 1-6 Angles 1
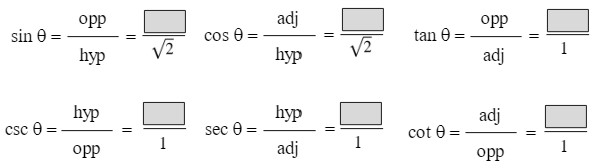
Answers:

Simplify the fractions as necessary.
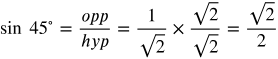
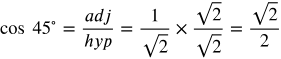
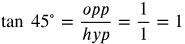
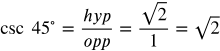
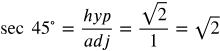
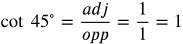
Frequently Used Angles 2
Use the equilateral triangle shown to find the exact values of the trigonometric functions for 30° and 60°.
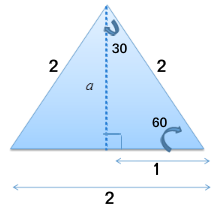
Use the Pythagorean theorem to find the length of the height of the triangle.

Let's start by finding the values for 30°. Now that we know the lengths of all sides of the triangle, we can solve the ratios by plugging in the values for the sides.
Trig Function 1-6 of 30° Angle
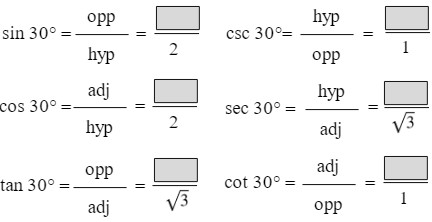
Answers:
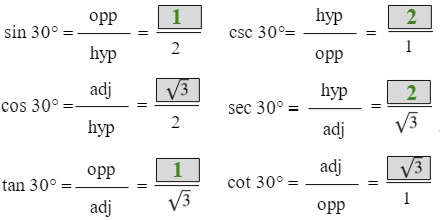

At this point, we will simplify the values we found as needed to eliminate the square root terms from the denominator. To simplify a fraction with a radical in the denominator, you multiply both the numerator and the denominator by the radical.

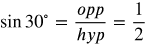
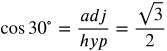
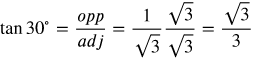
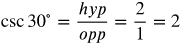
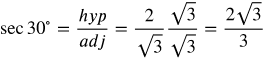
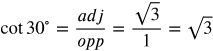
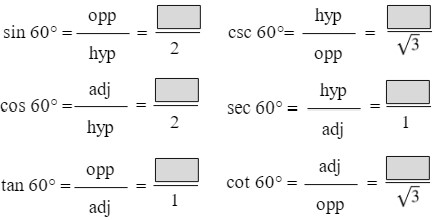
Trig Function 1-6 of 60° Angle
Use the equilateral triangle shown to find the exact values of the trigonometric functions for 30° and 60°.
Now let's find the values for the 60° angle.

Answers:
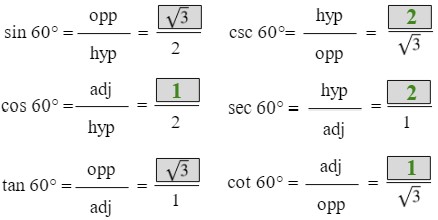
At this point, we will simplify the values we found as needed to eliminate the square root terms from the denominator. To simplify a fraction with a radical in the denominator, you multiply both the numerator and the denominator by the radical.
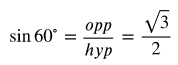
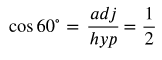
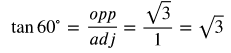
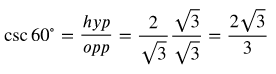
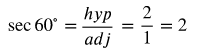
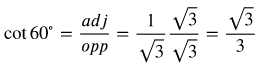
Sines, Cosines, and Tangents of Special Angles
| Degree | Radians | Sin θ | Cos θ | Tan θ |
|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0 |
| 30° | ||||
| 45° | 1 | |||
| 60° | ||||
| 90° | 1 | 0 | undefined |
Note:
sin 30° = ![]() = cos 60°
= cos 60°
and
sin 60° = ![]() = cos 30°
= cos 30°
Trigonometric Identities
From the preceding, the fundamental trigonometric identities can be defined by looking at the relationships between the functions and the three sides.
Reciprocal Identities
![]() : cos θ (
: cos θ (![]() ), sin θ (y)
), sin θ (y)
![]() : sec θ (
: sec θ (![]() ), cos θ (x)
), cos θ (x)
![]() : cot θ (
: cot θ (![]() ), tan θ (
), tan θ (![]() )
)
Quotient Identities
![]() : tan θ (
: tan θ (![]() ), sin θ (y), cos θ (x)
), sin θ (y), cos θ (x)
![]() : cot θ (
: cot θ (![]() ), cos θ (x), sin θ (y)
), cos θ (x), sin θ (y)
You can use these identities to simplify expressions or to solve problems.
Try it now! Use the trigonometric identities to transform the left side of the equation into the right side of the equation.
tan θ × cos θ = sin θ
What trig identity can be substituted for tan?
![]() cos θ = sin θ
cos θ = sin θ
Simplify.
sin θ = sin θ
cos θ and cos θ cancel out
Cofunction Relationships Example
sin 20° = .342
Find cos 70°
70 + 20 = 90 so the sin and cos are cofunctions.
cos(90° − θ) = sin θ
θ = 20
then cos(90° − 20°) = sin 20°
cos 70° = sin 20°
cos 70° = .342