Try It

Radian and Degree Measures Practice

Practice: Angles and Quadrants

Match the angle to the correct quadrant.

Refer to the radian and degree measure circle created in the lesson.

Remember, negative angles move clockwise!

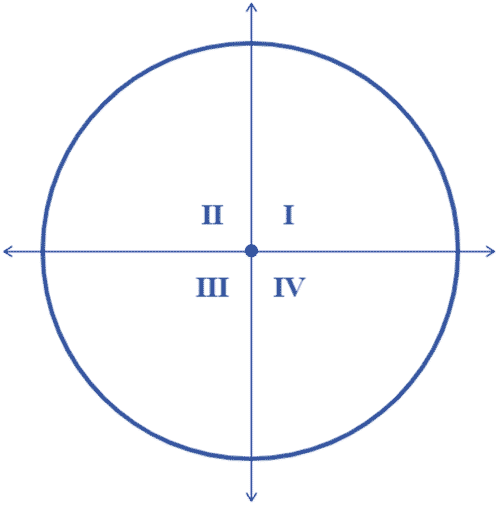
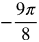
  • negative 9 pi over 8
  • −278°
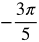
  • negative 3 pi over 5
  • −230°
  • −5
  • −66°
  • −1.4
  • −110°

Answer:

Practice: Converting Degrees and Radians

Convert 87°45′ to radians. Round your answer to 3 decimal places.

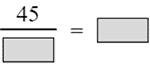
  • First, change 45′ to a decimal  the fraction with numerator 45 and denominator blank space equals blank space
  • Tip: Fractional parts of degrees are expressed in minutes and seconds, using prime (′) and double prime (″) as notations.
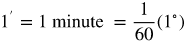
  • 1 foot equals 1 minute equals 1 over 60 times open paren 1 degrees close paren
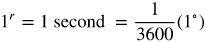
  • 1 to the rth power equals 1 second equals 1 over 3600 times open paren 1 degrees close paren
  • Answer: 45 over 60 equals .75

  • Add the minutes to the total degrees to find the angle measure in decimal form.

  • ____(Fill in the blank)°

  • Answer: 87.75°

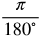
  • Multiply by the fraction with numerator pi and denominator 180 degrees

  • ____(Fill in the blank)° x 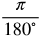the fraction with numerator pi and denominator 180 degrees = ____ (Fill in the blank) radians

  • Answer: 87.75° x 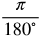the fraction with numerator pi and denominator 180 degrees = 1.532 radians

Practice: Arc Length and Area of a Sector

Find the arc length and area of a sector of a circle with a radius of 15 m and central angle of 65°

Arc length formula: s = rθ, where θ must be in radian measure

  • s = ____(Fill in the blank)m (____(Fill in the blank)°) 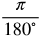the fraction with numerator pi and denominator 180 degrees= ____(Fill in the blank)m

  • Answer: s = 15m (65°) 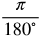the fraction with numerator pi and denominator 180 degrees=17.017m

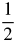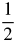  • Area of a sector formula: A = one halfr2θ

  • A = one half(____(Fill in the blank)m)2 (____(Fill in the blank)°) 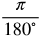the fraction with numerator pi and denominator 180 degrees = ____(Fill in the blank)m2

  • Answer: A = 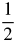one half(15m)2 (65°) 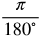the fraction with numerator pi and denominator 180 degrees = 127.627m2