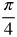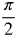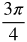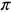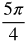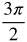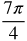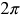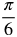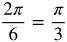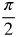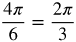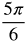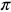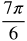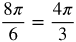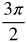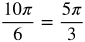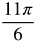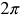Learn
Angles
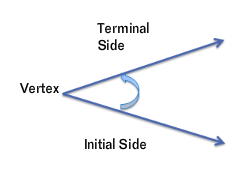
An angle is determined by rotating a ray about its endpoint.
The endpoint of the ray is called the vertex.
The starting position of the angle is called the initial side.
The position after rotation of the ray is called the terminal side.
Standard Position
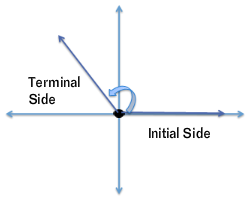
An angle can be placed in standard position in the coordinate system if:
- the vertex is at the origin
- the initial side is on the positive x-axis
Positive Angles
Positive angles are generated by a counterclockwise rotation.
Negative Angles
Negative angles are generated by a clockwise rotation.
Coterminal Angles
When angles have the same initial and terminal side, they are called coterminal angles.
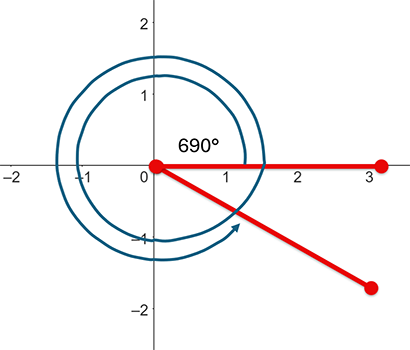
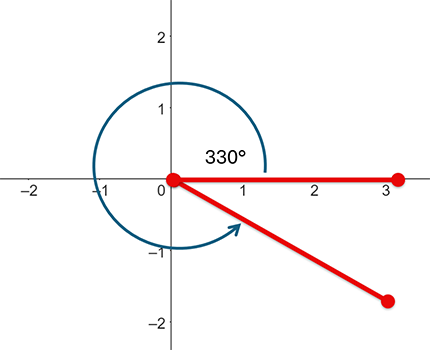
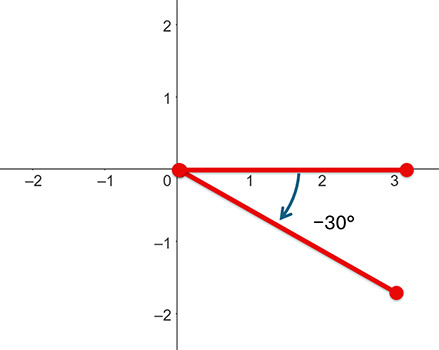
690˚, 330˚ and −30˚ are all coterminal angles.
You can find coterminal angles by adding or subtracting 360˚ from any angle.
Degree Measure
One way to measure angles is using degrees. Look at a circle in reference to degree measure. Rotation from the initial side all the way around to the initial side again is 360 degrees.
To put it another way, 1 degree is
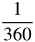rotation around the vertex.
Degree Measure and Rotation
Look over each formula and watch the video of rotation.
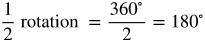
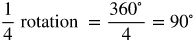
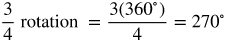
Degree Measure by Eighths
Now let's fill in the common angles. Divide the circle into 8 equal parts.
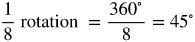
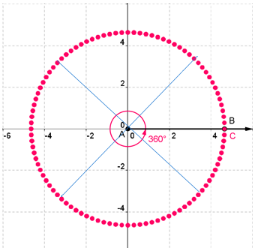
Think about where the following degree measurements belong in the circle.
Measurements
- 0°
- 45°
- 90°
- 135°
- 180°
- 225°
- 270°
- 315°
- 360°
Degree Measure by Twelfths
Now let's fill in the common angles. Divide the circle into 12 equal parts.
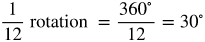
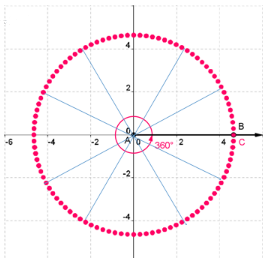
Think about where the following degree measurements belong in the circle.
Measurements
- 0°
- 30°
- 60°
- 90°
- 120°
- 150°
- 180°
- 210°
- 240°
- 270°
- 300°
- 330°
- 360°
Degrees, Minutes, and Seconds
Degrees can be broken down into smaller units of measure called minutes and seconds.
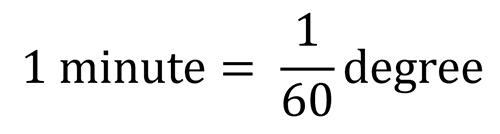
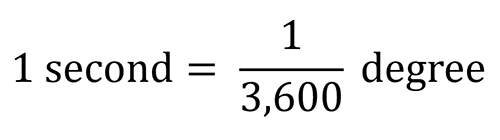
Minutes and seconds are notated using single or double apostrophes respectively.
Example: 60 degrees, 10 minutes, and 12 seconds = 60°10'12''.
Converting DMS to Decimal Form
Sometimes it is necessary to convert an angle measure given in degrees, minutes, and seconds (DMS) to decimal form.
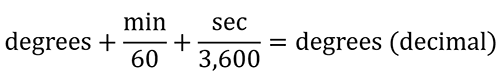
Example:
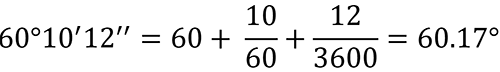
Radian Measure
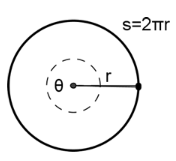
Another way of measuring angles is radian measure.
Since the circumference of a circle is 2r, then there are 2 radians around a circle.
Definition of a radian: One radian is the measure of an angle in standard position that intercepts an arc s equal in length to the radius r of the circle.
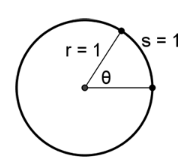
Radian Measure
The circumference of a circle is 2r so one complete revolution would be s = 2r or
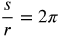
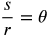
where θ is measured in radians
The units of measure for s and r are the same, so this ratio has no unit. It is simply a real number.
Radian Measure and Rotation
Look over each formula and watch the video of rotation.
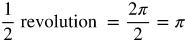
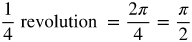
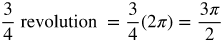
Radian Measure by Eighths
Now let's fill in the common angles. Divide the circle into 8 equal parts.
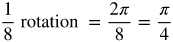
Think about where the following measurements belong in the circle.
Measurements
Radian Measure by Twelfths
Now let's fill in the common angles. Divide the circle into 12 equal parts.
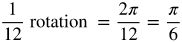
Think about where the following measurements belong in the circle.
Measurements
Radian and Degree Measure
Let's add radian measures to the circle.
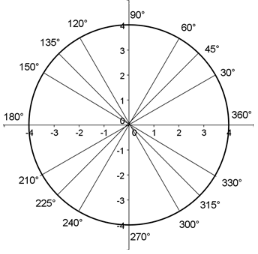
Think about where the following measurements belong in the circle.
Measurements
Changing from Degrees to Radians and Radians to Degrees
Open Changing from Degrees to Radians and Radians to Degrees in a new tab
Finding the Arc Length and Area of a Sector
Arc length = s = distance from A to B
Arc Length:
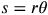
Area of a Sector:
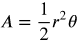
Measurements for arc length and area of a sector must be in radian measure.
Calculate Arc Length of a Circle and the Area of a Sector of a Circle
Open Calculate Arc Length of a Circle and the Area of a Sector of a Circle in a new tab