Try It
Exponential Growth and Decay Practice
Practice 1
Complete the table to determine the balance A for an investment of $15,000 at an interest rate of 8% for 25 years compounded n times a year.
| n | 1 | 2 | 4 | 12 | 365 | Continuously |
| A |
Answer:
| n | 1 | 2 | 4 | 12 | 365 | Continuously |
| A | 102,727.13 | 106,600.25 | 108,669.69 | 110,102.64 | 110,811.55 | 110,835.84 |
When you have completed the table, look at the difference 25 years has made to the amount of money invested.
Look at the difference it makes when we change the number of times a year the interest was compounded.
Practice 2
Five hundred grams of Plutonium is stored in a container. The decay rate for Plutonium is 0.012% per year. How much Plutonium is left after 1000 years?
Identify the following:
- Initial amount:______(Fill in the blank) grams
- Decay factor:______(Fill in the blank) %
- Time:______(Fill in the blank) years
- P = ______(Fill in the blank)(1 −______(Fill in the blank))
- P = ______(Fill in the blank) grams
Write a model where P = the population after 10 years using the formula
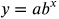
______(Fill in the blank)
Answer:
- Initial amount: 500 grams
- Decay factor: 0.012% = 0.00012
- Time: 1000 years
- P = 500 (1 − 0.00012)
- P = 443.457 grams
Write a model where P = the population after 10 years using the formula
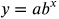
1000
Practice 3, Part One
In 2000, the tuition to attend a state university was $5,000. The average increase per year since has been 6.2%. How long will it take for tuition to double?
Identify the following:
- Initial amount: $______(Fill in the blank)
- Growth factor:______(Fill in the blank) %
- Amount after it doubles: $______(Fill in the blank)
- ______(Fill in the blank) = ______(Fill in the blank) (1 + ______(Fill in the blank))t
- Divide both sides by 5000: ______(Fill in the blank) = (1 + 0.062)t
- Change to logarithm form.
- log ______(Fill in the blank) ______(Fill in the blank) = ______(Fill in the blank)
Write a model for the tuition using the formula
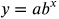
Answer:
- Initial amount: $5000
- Growth factor: 6.2% = 0.062
- Amount after it doubles: $10,000
- 10,000 = 5,000 (1 + .062)t
- Divide both sides by 5000: 2 = (1 +0 .062)t
- Change to logarithm form.
- log 1.062 2 = t
Write a model for the tuition using the formula
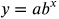
Practice 3, Part Two
In 2000, the tuition to attend a state university was $5,000. The average increase per year since has been 6.2%. How long will it take for tuition to double?
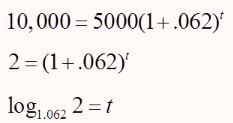
- Use change-of-base formula
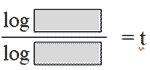
- t = ______(Fill in the blank) years rounded to the nearest year
Answer:

- t = 12 years rounded to the nearest year