Learn
Exponential Growth and Decay
Exponential Growth
The function 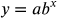 shows exponential growth
if and only if
shows exponential growth
if and only if
a > 0
b > 1
b is the rate of growth
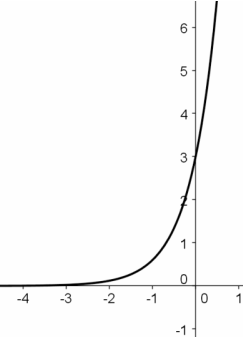
Example:
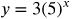
5 is the rate of growth
Exponential Decay
The function 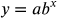 is exponential decay if and only if
is exponential decay if and only if
a > 0
0 < b < 1
b is the rate of decay
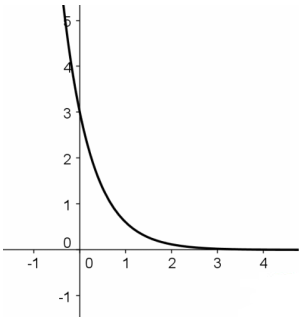
Example: 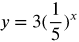
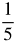 is the rate of decay
is the rate of decay
Compound Interest
One very common use for the exponential function is the growth of an investment earning interest that is compounded at various time intervals.
The growth rate is 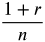
The compound interest formula is 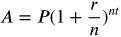
- P is the initial amount, or the principle of the account.
- r is the annual percentage rate (APR) expressed as a decimal
- t is the number of years
- n is the number of times compounded per year
- A is the amount in the account after t years
Compound Interest
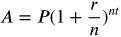
n is the number of times compounded per year
The following terms with help you understand the terminology used with compounding interest n times a year.
- Annually: n = 1
- Semi-annually: n = 2
- Quarterly: n = 4
- Monthly: n = 12
- Weekly: n = 52
- Daily: n = 365
Continuous Compounding
If we compound more and more frequently so that n gets very, very large, we say that we are compounding continuously.
Continuous Compound Interest Formula: 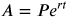
- P is the initial amount
- r is the annual rate expressed as a decimal
- t is the number of years
- A is the amount after t years
- e is the natural base
Using Compound Interest and Continuous Compound Interest
Open "Using Compound Interest and Continuous Compound Interest" in a new tab