2.09 Graphs of Rational Functions

Try It

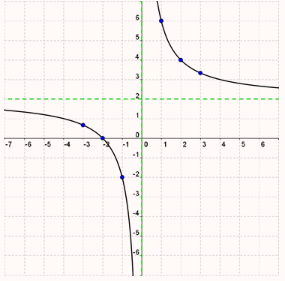
Graphs of Rational Functions

Domain, Range, and y-intercept

Sketch the graph of the rational function

Find the domain and range of the rational function.

• Domain: all real numbers except 2x = 0 and x = 0
• Range: all real numbers except y = 2

Find and plot the y-intercept by finding f(0).

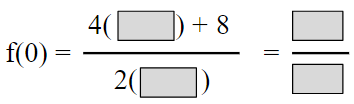
x-intercept

We continue with the same function, moving on to sketch any x-intercepts.

Sketch the graph of the rational function

Find and plot the x-intercepts by letting f(x) = 0.

• Check Answer =
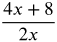
• Check Answer = 4x + 8
• Check Answer = 4x
• Check Answer = x
• x-intercept: (−2, 0)

Vertical Asymptote

We continue with the same function, moving on to sketch any vertical asymptotes.

Sketch the graph of the rational function

Find and draw the vertical asymptote(s). Sketch the asymptote(s) on your own paper, then check your answer here.

• Check Answer = 2x
• Check Answer = x

Discontinuities and Horizontal Asymptotes

We continue with the same function, moving on to sketch any discontinuities and horizontal asymptotes.

Sketch the graph of the rational function

Find the discontinuities. Check Answer

Find and draw the horizontal asymptotes.

• The degree of the numerator equals the degree of the denominator.
• 
• 

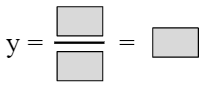
Slant Asymptote

We continue with the same function, moving on to sketch any slant asymptotes.

Sketch the graph of the rational function

Find and draw the slant asymptotes. Check Answer

Points on the Left

We continue with the same function, moving on to sketch the points on the left of the graph.

Sketch the graph of the rational function

Find the intervals of increasing and decreasing on the left of the vertical asymptote. Graph each point.

x		f(x)
−1		Check Answer
−2		Check Answer
−3		Check Answer

Points on the Right

We continue with the same function, moving on to sketch the points on the right of the graph.

Sketch the graph of the rational function

Find the intervals of increasing and decreasing on the left of the vertical asymptote. Graph each point.

x		f(x)
1		Check Answer
2		Check Answer
3		Check Answer

Intervals of Increasing and Decreasing

We continue with the same function, finding the intervals of increasing and decreasing.

Sketch the graph of the rational function

• Increasing: never
• Decreasing: (−∞, 0) and (0, ∞)

Maximum, Minimum, and Symmetry

Finally, we find the maximum and minimum points, and test for symmetry.

Sketch the graph of the rational function

• Find the maximum and minimum points. Check Answer
• Test for symmetry.
  
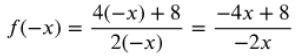
  There is no symmetry.

Our final graph of the function looks like this: