2.08 Identify Discontinuity

Try It

Identify Discontinuity

Practice 1

Determine whether the function is continuous or discontinuous.
f(x)= x²−2x + 1

Continuous Discontinuous

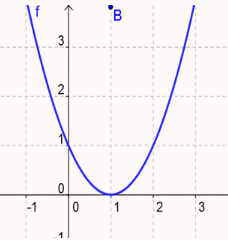
Practice 2

Determine whether the function is continuous or discontinuous.

Continuous Discontinuous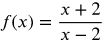

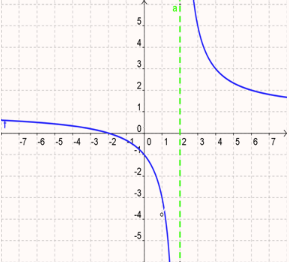
Practice 2

• Find the x-values (if any) at which the function is not continuous.
• Decide if discontinuities are removable.
• Find intervals of continuity. 

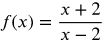
The function is discontinuous at:
x − 2 = 0

x = Check Answer

Intervals of continuity:
(−∞,Check Answer ) and (Check Answer , ∞)

Practice 3

Determine whether the function is continuous or discontinuous.

Continuous Discontinuous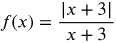

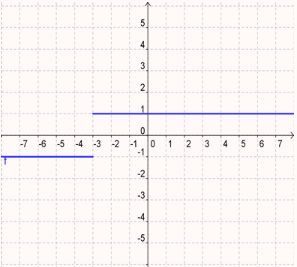
Practice 3

• Find the x-values (if any) at which the function is not continuous.
• Decide if discontinuities are removable.
• Find intervals of continuity.

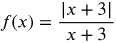
The function is discontinuous at:
x + 3 = 0

x = Check Answer

Intervals of continuity:
(−∞, Check Answer ) and (Check Answer , ∞)

Practice 4

Determine whether the function is continuous or discontinuous.

Continuous Discontinuous

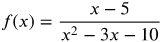
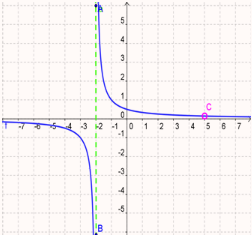
Practice 4

• Find the x-values (if any) at which the function is not continuous.
• Decide if discontinuities are removable.
• Find intervals of continuity.

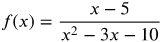
The function is discontinuous at:
x² − 3x − 10= 0

(x − Check Answer )(x + Check Answer ) = 0

x − Check Answer = 0 and x + Check Answer = 0

x = Check Answer x = Check Answer

The function is discontinuous at x = 5 and x = −2.

Intervals of continuity:
(−∞, Check Answer ), (Check Answer , Check Answer ),

and (Check Answer , ∞)