2.08 Identify Discontinuity

Learn

Identity Discontinuity

Continuity

A function is continuous on an open interval (a, b) if it is continuous at each point in the interval. A function that is continuous from (−∞, ∞) is everywhere continuous.

Informally, a function is continuous if the graph can be drawn from one end to the other without lifting your pencil.

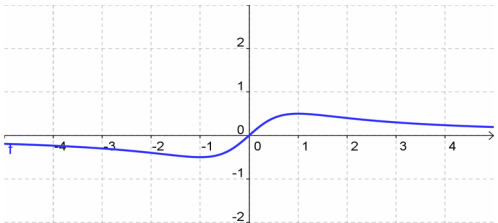
The graph of this function is continuous from (−∞, ∞) or everywhere continuous.

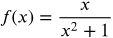
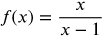
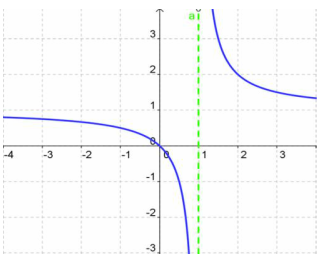
This function is not continuous because it is undefined at x = 1

The function is continuous on the interval (−∞, 1) and the interval (1, ∞)

Graph the following functions on your calculator.

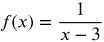
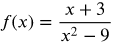
Note that the two graphs appear identical.

As you can see, looking at the graph does not tell you everything about the functions.

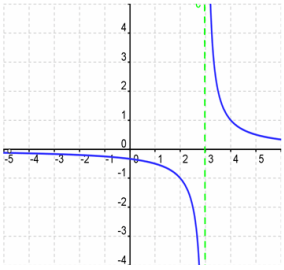
Let's look at the asymptotes for the functions from the previous slide.

Vertical asymptotes for the second equation would be x² − 9 = 0
x² = 9

x = ±3

Why doesn't the graph show a vertical asymptote at −3?

To find out, let's simplify both equations.

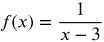
This equation is already in its simplest form.

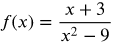
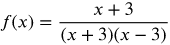
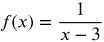
After simplifying, we can see that the two equations are the same. x= −3 is called a removable discontinuity in the second equation. This means that for the second equation, there is a hole in the graph at x= −3.

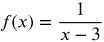
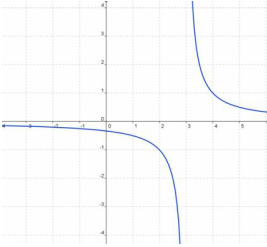
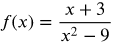
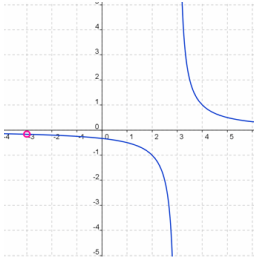
The graphs are not identical.