Learn
Relative Minimums and Maximums
Increasing or Decreasing
Look at the graph of the function f(x) = x³ − 3x² +2 .
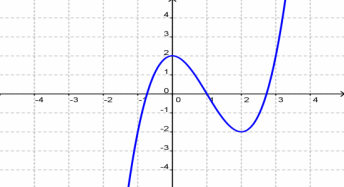
In the last section, we determined the intervals of x-values for which the function is increasing, decreasing, or constant.
Relative Minimum and Maximum

Moving from left to right, on the x-axis, the intervals are:
- Increasing: (−∞, 0)
- Decreasing: (0, 2)
- Increasing: (2, ∞)
On this graph, (0, 2) is a relative maximum because it is the highest point in its section of the graph. It is a place where the graph shifts from increasing to decreasing.
Likewise, (2, −2) is a relative minimum because it is the lowest point in its section of the graph. It is a place where the graph shifts from decreasing to increasing.
Please note: Please note: Endpoints can only be extrema if the interval is closed. In other words, if the function goes on forever in either direction (to infinity or negative infinity), then there are no endpoints to consider, so they cannot be extrema.
Now look at the function f(x) = x + 3.
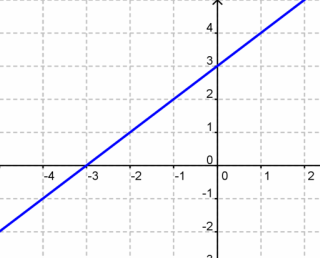
This function is always increasing from (−∞, ∞).
There are no points where this function goes from increasing to decreasing or from decreasing to increasing.
There are no relative minimum or maximum points in the graph of this function.
Now look at the function f(x) = x² − 2x − 3 .
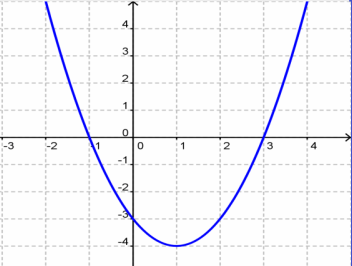
This graph:
- decreases on the interval (−∞, 1)
- increases on the interval (1, ∞)
and has a relative ____________ minimum at (1, −4).