Learn
Transformations Rules
| Translations in the Coordinate Plane | |
|---|---|
| Translation | (x, y) →(x ± a, y ± b) |
a represents the number of units the figure will be translated left or right.
b represents the number of units the figure will be translated up or down.
Reflections Rules
| Reflections in the Coordinate Plane | |
|---|---|
| Reflection across the x-axis | (x, y) → (x, −y) |
| Reflection across the y-axis | (x, y) → (−x, y) |
| Reflection across the line y = x | (x, y) → (y, x) |
Rotation Rules
| Rotations in the Coordinate Plane (clockwise) | |
|---|---|
| Rotation 90° | (x, y) → (y, −x) |
| Rotation 180° | (x, y) → (−x, −y) |
| Rotation 270° | (x, y) → (−y, x) |
Compositions of Transformations
A composition of transformations is a transformation that is formed from a combination of transformations. In other words, it a transformation followed by other transformations.
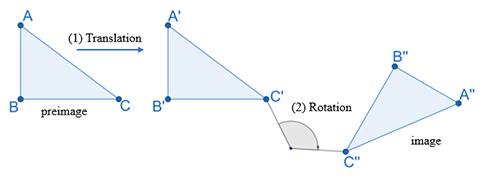
The diagram shows a composition of transformations in which ∆ABC is translated to the right and then rotated.
Double Prime Notation
Anytime you have three figures of a composition of transformations, the second figure is labeled as primes after the letters. Prime notation has an apostrophe (') after the letters. The third figure is labeled as double primes after the letters. Double prime notation has two apostrophes ('') after the letters.
For example, in the image below, if the first figure is ABC, then the second figure is A’B’C’ and the third figure is A”B”C”. ABC is the preimage and A”B”C” is the image.

Compositions of Two Translations
A composition of two translations is a translation after a translation. The final image represents the composition of the translations. The composition of two translations is the same as a translation of the preimage.
To get the vertical transformation of the preimage to the image, you will need to find the sum of the two vertical translations.
To get the horizontal translation of the preimage to the image, you will need to find the sum of the two horizontal translations.
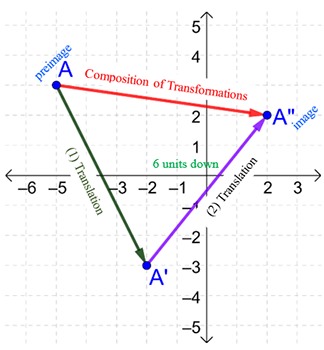
In the diagram, point A is translated 3 units right and 6 units down. Then, translated 4 units right and 5 units up. The image A”B”C” is the result of the two translations, the composition of the transformations.
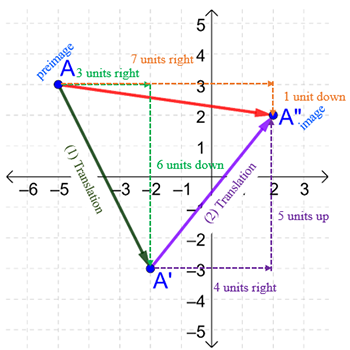
Note: The composition of the two translations is a translation of the preimage 7 units right and 1 unit down. Find the sum of the two horizontal translations ((+3) + (+4)) to get the horizontal translation (+7) of the preimage to the image. Find the sum of the two vertical translations ((−6) + (+5)) to get the vertical translation (−1) of the preimage to the image.
Glide Reflections
A glide reflection is an image that is formed by a translation of a figure, followed by a reflection of the translation of the figure. It can also be an image that is formed by a reflection of a figure, followed by a translation of the reflection of the figure.
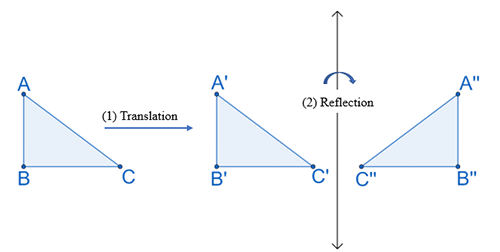
Example #1
Watch Graph a Composition of Transformations.
Open Graph a Composition of Transformations in a new tab
Example #2
Watch Graph a Composition of Transformations.
Open Graph a Composition of Transformations in a new tab
Reflections Over Two Parallel Lines Theorem
The Reflection Over Two Parallel Lines Theorem states that:
A reflection of a figure over a line followed by a reflection over a line that is parallel to that line is the same as a one translation of the figure.
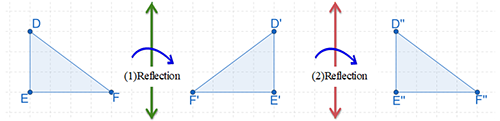
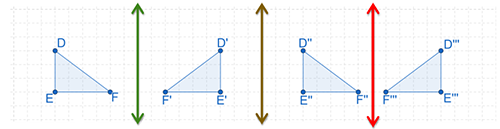
A reflection of a figure over a line followed by a reflection over a line that is parallel to that line, followed by another reflection over a third line is the same as a one reflection of the figure.
Reflections Over Intersecting Lines Theorems
The Reflection Over Two Intersecting Lines Theorem states that a composition of reflections of a figure over two intersecting lines is the same as a one rotation of the figure.
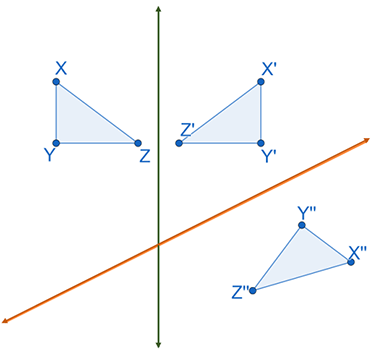
Application
Composition of Transformations and Congruence
The rigid motions that hold congruence are translations, reflections, and rotations. If an image is the result of a rigid transformation or a composition of rigid transformations on a figure, then it is congruent to the original figure (preimage).
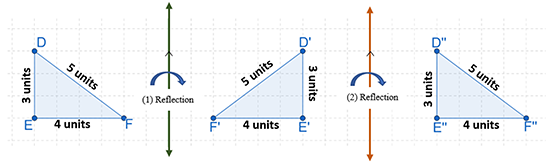
Example #3
Watch Determine Congruence Using Transformations.
Open Determine Congruence Using Transformations in a new tab