Learn

Transformations

We have studied triangles and quadrilaterals in depth. In this lesson we will focus on how to transform geometric figures.

Here's a list of the important vocabulary you will learn:

  • Image
  • Preimage
  • Isometry
  • Transformation
  • Translation
  • Reflection
  • Rotation

A transformation is a move of an object or figure. There are some basic terms you need to know before we go over the different types of transformations.

The original figure before the transformation is called the preimage. The new figure after the transformation is called the image.

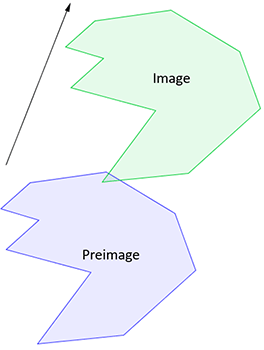
abstract preimage and abstract image. They are the same size, but in different locations and different colors. An arrow indicates the movement of the preimage shape to the image shape.

Isometry

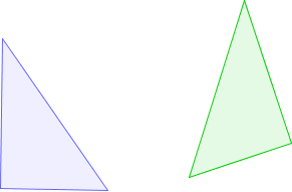
A figure is said to have isometry if the figure is the same size after the transformation. Below are illustrations of transformations in which one has isometry and one that does not.

Isometry: This figure has isometry because the size of the shape is the same after the transformation.

Two triangles that are in different locations but are the same size and have the same angle measures. The purple triangle preimage is on the left. The green triangle image is flipped and turned slightly, compared to the purple preimage.

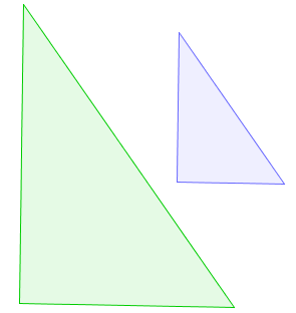
Not Isometry: This figure does not have isometry because the size of the shape is not the same after the transformation.

Two triangles that are in different locations. While they have the same angle measures, they are different sizes. The green triangle is larger and the purple triangle is smaller.

Example #1

Do the figures have isometry?

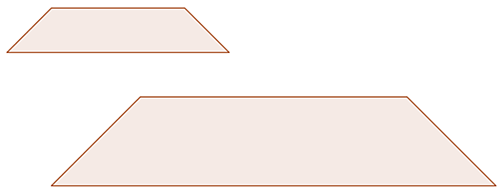
two trapezoids that are different sizes

Answer: They do not have isometry because they are not the same size.

Types of Transformations

Remember, a transformation is just a move of an object. You will learn three types of transformations throughout this unit:

  • Translation
  • Reflection
  • Rotation

Each of these transformations will always have isometry. You will see that, even though a transformation of one of the types above has been made, the size of the figure will stay the same.

Translations

A translation is a movement of a figure around a given plane. This can be a movement left, right, up, or down or a combination of these movements. The two examples below represent translations. A translation is an isometry.

A purple sun preimage on the left with a replicated purple sun image moved up and to the right. The suns are the same size. An arrow between the two suns indicates the movement of the image upwards and to the right of the preimage.
A purple smiley face preimage on the left with a replicated purple smiley face image moved slightly up and to the right. The smiley faces are the same size. An arrow between the two smiley faces indicates the movement of the image upwards and to the right of the preimage.

Translation Notation

The notation for a translation shows how a figure will be translated within the coordinate plane.

(x, y) → (x ± a, y ± b)

  • a represents the number of units the figure will be translated left or right.
  • b represents the number of units the figure will be translated up or down.

Example #2

Determine the number of units a figure would be translated left, right, up, or down.

(x, y) → (x + 2, y − 3)

  • The figure will be translated 2 units right because you have x + 2. If it were x − 2, you would translate the figure left two units.
  • The figure will be translated 3 units down because you have y − 3. If it were y + 3, you would translate the figure up 3 units.

Example #3

Determine the number of units a figure would be translated left, right, up, or down.

(x, y) → (x − 7, y + 5)

The figure will be translated ___blank units ___ blank(left or right).

  • Look at the "x" part of the notation. How many units will the figure be translated and will it be left or right?
  • Answer: The figure will be translated 7 units left because you have x − 7.

The figure will also be translated ___blank units ___ blank(up or down).

  • Look at the "y" part of the notation. How many units will the figure be translated and will it be up or down?
  • Answer: The figure will also be translated 5 units up because you have y + 5.

Example #4

Determine the number of units a figure would be translated left, right, up, or down.

(x, y) → (x, y − 6)

The figure will be translated ___blank units ___blank (left or right).

  • Look at the "x" part of the notation. How many units will the figure be translated and will it be left or right?
  • Answer: The figure will be translated 0 units because you have just x.

The figure will also be translated ___blank units ___blank (up or down).

  • Look at the "y" part of the notation. How many units will the figure be translated and will it be up or down?
  • Answer: The figure will also be translated 6 units down because you have y − 6.

Translations on a Coordinate Plane

Sometimes you just want to move a picture or object over. This is a translation. You will have to know if you want to move to left (negative value ←) or right (positive value →) and if you want to move up (positive value ↑) or down (negative value ↓).

Prime Notation

Anytime you have two figures of a translation, the second figure is labeled as primes after the letters. Prime notation has a ' (an apostrophe) after the letters.

For example, if the first figure is ABC, then the second figure is A'B'C'.

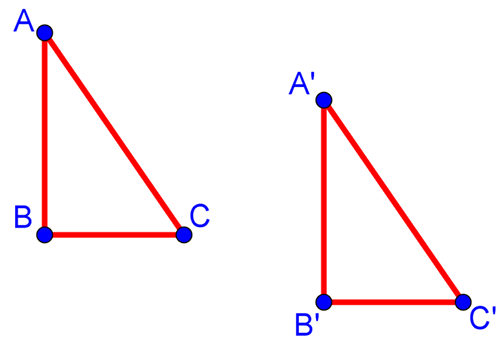
A Triangle with Points A, B, and C and a second triangle that is the same size as Triangle ABC but in a different location (downwards and to the right of the preimage). This second triangle has Points A', B', and C' or Points A prime, B prime, and C prime and is called Triangle A'B'C'.

Example #5

For example, this figure is translated 4 right and down 1. Notice the notation for B and B'.

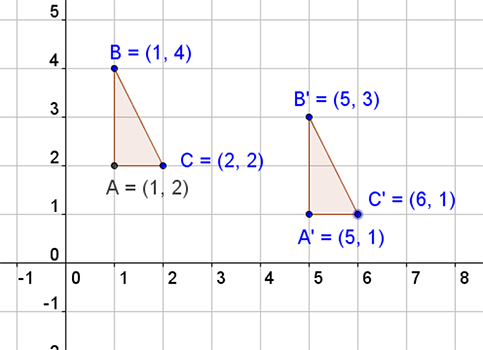
Triangle ABC on a coordinate plane with Point A at (1,2), Point B at (1,4), and Point C at (2,2). A translation of Triangle ABC is down and to the right and it is called Triangle A'B'C' or Triangle A prime B prime C prime. It has Point A ' or A prime at (5,1), Point B' or Point B prime at (5,3), and Point C' or C prime at (6,1).
See larger version of Example #5 graph here.

Notice what happens to each point as it is translated right 4 and down 1:

  • A(1,2) → A'(5,1)
    • (1 + 4, 2 − 1) = (5, 1)
    • Notice that we added 4 to the x-value (which went right) and subtracted 1 from the y-value (which went down).
  • B(1,4) → B'(5,3)
    • (1 + 4, 4 - 1) = (5, 3)
    • Notice that we added 4 to the x-value (which went right) and subtracted 1 from the y-value (which went down).
  • C(2,2) → C'(6,1)
    • (2 + 4, 2 - 1) = (6, 1)
    • Notice that we added 4 to the x-value (which went right) and subtracted 1 from the y-value (which went down).