Learn
Transformations
We have studied triangles and quadrilaterals in depth. In this lesson we will focus on how to transform geometric figures.
Vocabulary:
- image
- preimage
- isometry
- reflection
- translation
- rotation
A transformation is a move of an object or figure.
There are some basic terms you need to know before we go over the different types of transformations.
The original figure before the transformation is called the preimage.
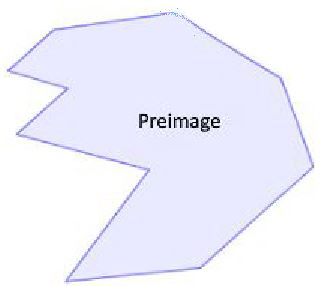
The new figure after the transformation is called the image.
Isometry
A figure is said to have isometry if the figure is the same size after the transformation. Below are illustrations of transformations in which one has isometry and one that does not.
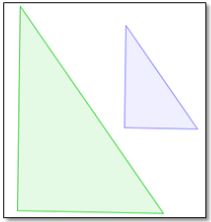
not isometry
isometry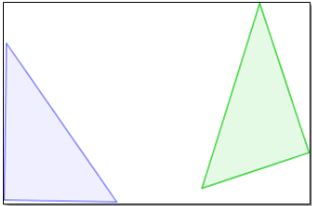
Example #1
Do the figures have isometry? Yes or No?
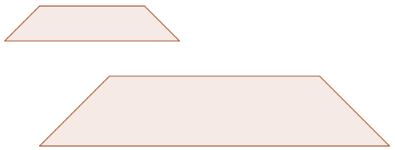
Answer: No, these figures do not have isometry. Even though they are the same shape, they are not the same size.
Transformations
Reminder: transformation is just a move of an object.
You will now learn three types of transformations:
- reflection
- rotation
- translation
Each of these transformations will always have isometry. You will see that even though a transformation of one of the types above has been made, the size of the figure will stay the same.
Reflections
The first transformation that we will investigate is a reflection. A reflection in general terms is a flip on an object. A reflection is also known as the mirror image.
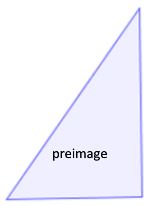
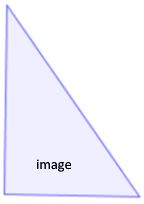
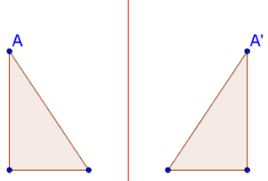
As described before, a reflection is a flip of an object. Typically the flip is over a line that is away from the object as shown below. This line is referred to as the line of reflection. You should notice that corresponding points such as A and A' are the same distance from the line of reflection.
Line of Refection
There are times when the line of reflection is not away from the figure but instead intersects the object as shown below.
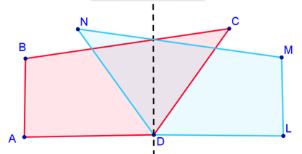
Math Open Reference: Reflection – of a line segment is a good interactive showing a line segment being reflected. Move a point to see how the corresponding point reacts to your move.
See how moving the line of reflection affects the image by going to GeoGebra: ACCESS - Line of Reflection.
How to Name a Reflection
There is a specific way to name a transformation. To describe this reflection in notation form we would say Figure ABCD --> Figure WXYZ. The important thing to remember is that you must have the corresponding vertices in the figures be in the same location in the notation.
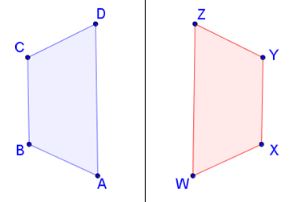
For instance vertex A on the left diagram corresponds with vertex W on the right diagram and they are both listed first in the notation. You will be counted off for not following this rule.
Lines of Symmetry
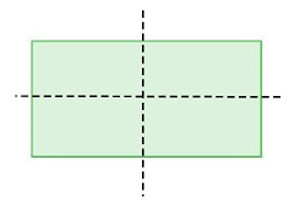
Another concept of reflection is line symmetry. A figure has line symmetry if a line can be drawn through the figure where the figure maps on to itself perfectly when folded over the line.
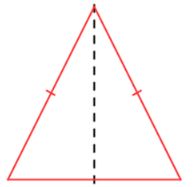
Figures can have zero or multiple lines of symmetry as shown below.
 two lines of symmetry
two lines of symmetry
 no lines of symmetry
no lines of symmetry
Website
Math Open Reference: Reflection is a good interactive showing a line segment being reflected. Move a point to see how the corresponding point reacts to your move.
Rotations
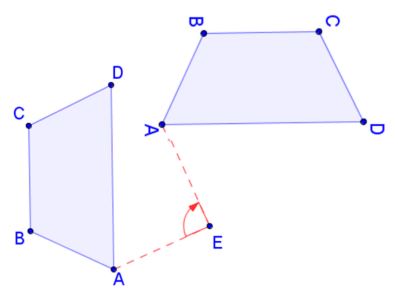
The next transformation we will investigate is rotation. A rotation is a turn of an object about a point.
Turns
You can turn to the right, which is clockwise.
You can turn to the left, which is counterclockwise.
We will focuse on 90° 180° and 270° turns.
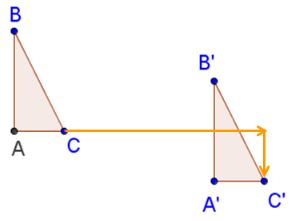
Translation
The last transformation that we will investigate in this lesson is translation. A translation is a slide of an object.
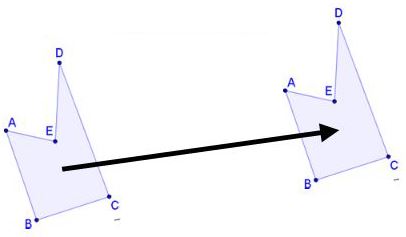
Translations can be described as a figure that has a slide.
Note the triangle ABC slides to the right and down. We'll look at this more in the next lesson when we look at transformations in the coordinate plane.