Learn
Trapezoids
A trapezoid is a quadrilateral with exactly one pair of parallel sides.
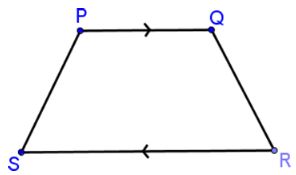
In looking at the picture you will see line segment PQ is parallel to segment SR
Those two segments are the bases.
Segment PS and segment QR are the legs ∠R and ∠S are base angles.
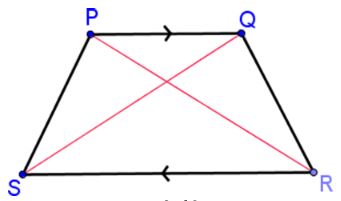
Segments SQ and RP are called diagonals
∠P is opposite ∠R and ∠S is opposite ∠Q
Go to GeoGebra: ACCESS -Trapezoid to find out more about trapezoids.
Trapezoids and Parallel
Because the bases of a trapezoid are formed by parallel lines, the consecutive angles on the same legs of the trapezoid have a special relationship. They are same side interior angles. Therefore, just as with same side interior angles formed by a transversal cutting two parallel lines, consecutive angles on the legs of a trapezoid are supplementary (sum to 180°) .
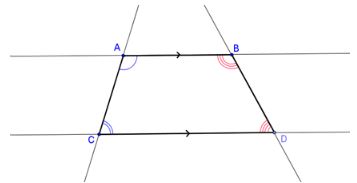
Go to GeoGebra: ACCESS -Consecutive Angles of a trapezoid to find out more!
Example #1
Segments AB and CD are __________.
- bases
- consecutive angles
- base angles
- diagonals
- legs
Answer: A - bases; AB and CD are parallel, so they form the base of the trapezoid.
Example #2
Segments DA and BC are __________.
- bases
- consecutive angles
- base angles
- diagonals
- legs
Answer: E - legs ; DA and BC are not parallel, so they form the legs of the trapezoid.
Example #3
Segments AC and BD are __________.
- bases
- consecutive angles
- base angles
- diagonals
- legs
Answer: D - diagonals; AC and BD cut through the interior of the trapezoid, so they are diagonals.
Example #4
∠A and ∠D are ________________.
- bases
- consecutive angles
- base angles
- diagonals
- legs
Answer: B - consecutive angles; Angle A and Angle D share a leg of the trapezoid as a side, so they are consecutive angles.
Example #5
∠C and ∠D are ____________.
- bases
- consecutive angles
- base angles
- diagonals
- legs
Answer: C - base angles; Angle C and Angle D share a base of the trapezoid as a side, so they are base angles.
Isosceles Trapezoids
An isosceles trapezoid is a trapezoid whose legs are congruent.
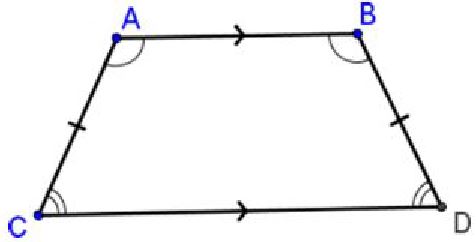
Go to Geogebra: Isosceles Trapezoids to find out more.
Isosceles Trapezoids Theorems
If a trapezoid is isosceles, then each pair of base angles is congruent.
If ABDC is a trapezoid and line segment AC ≅ line segment BD, then ∠A ≅ ∠B and ∠C ≅ ∠D.
You can use this theorem to find the measure of missing angles of a trapezoid, knowing that the interior angles of a quadrilateral sum to 360∘.
If a trapezoid has a pair of congruent base angles, then it is an isosceles trapezoid.
If ABDC is a trapezoid and ∠A ≅ ∠B and ∠C ≅ ∠D, then ABDC is an isosceles trapezoid and AC ≅ BD.
This is the converse of the previous theorem. It allows you to prove a trapezoid isosceles given the measures of its base angles. You can also use this theorem to find the length of a missing leg of a trapezoid, given the length of the other leg and congruent base angles.
A trapezoid is isosceles if and only if its diagonals are congruent.
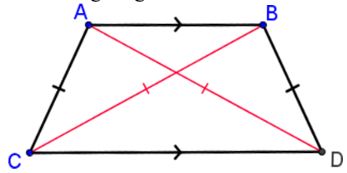
If ABDC is a trapezoid and line segment AD ≅ line segment BC, then ABDC is an isosceles trapezoid.
This theorem can be used to prove trapezoids are isosceles or to find the length of missing diagonals.
Example #6
Open Apply Properties of Isosceles Trapezoids to Find Unknown Angle Measures in a new tab
Example #7
Open Apply Properties of Trapezoids to Find Unknown Angle Measures in a new tab
Midsegement
A midsegment is the segment that connects the midpoints of the legs of a trapezoid.
Midsegement Theorem: The midsegment of a trapezoid is parallel to each base and its length is one half the sum of the lengths of its bases.
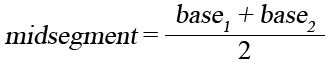
You can use this theorem to: Find the length of a base given the length of the midsegment and other base Find the length of the midsegment given the lengths of the bases Verify that a segment is the midsegment given the slopes of the bases and their lengths
Example #8
Open Find the Length of the Midsegment of a Trapezoid Given the Lengths of Its Bases in a new tab