Try It

Proving Quadrilaterals are Parallelograms Practice

Practice Problem #1

Is there enough information to prove the quadrilateral is a parallelogram?

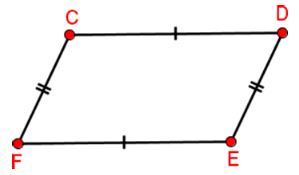
A 4-sided figure with opposite sides congruent

Answer: Yes

Which reason explains your answer?

  • One pair(s) of opposite sides are parallel and congruent
  • Both pairs of opposite sides are parallel
  • Both pairs of opposite sides are congruent
  • Both pairs of opposite angles are congruent
  • Consecutive angles are supplementary

Answer: Both pairs of opposite sides are congruent

Practice Problem #2

Is there enough information to prove the quadrilateral is a parallelogram?

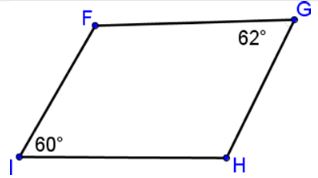
A 4-sided figure F G H I, The measure of angle G equals 62 degrees. The measure of angle I equals 60 degrees. Angles I and G are opposite angles.

Answer: No

Which reason explains your answer?

  • One pair(s) of opposite sides are parallel and congruent
  • Opposite sides are not parallel
  • Opposite sides are not congruent
  • Opposite angles are not congruent
  • Consecutive angles are not supplementary

Answer: Opposite angles are not congruent

Practice Problem #3

Show that C(-6, 2), D(-1, 3), E(2, -3), F(-3, -4) are vertices of a parallelogram. Use method 2, which is the slope formula to prove opposite sides are parallel.

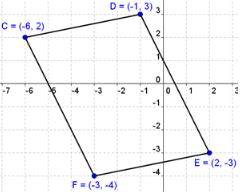
A 4-sided figure in a coordinate plane with vertices C(negative 6, 2), D(negative 1, 3), E(2, negative 3) and F(negative 3, negative 4)

Answer:

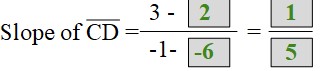
slope of CD equals the fraction with numerator 3 minus 2 and denominator negative 1 minus negative 6 equals one-fifth
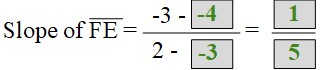
slope of FE equals the fraction with numerator negative 3 minus negative 4 and denominator 2 minus negative 3 equals one over 5
slope of CF equals the fraction with numerator negative 4 minus 2 and denominator negative 3 minus negative 6 equals negative 6 over 3 equals negative 2
slope of DE equals the fraction with numerator negative 3 minus 3 and denominator 2 minus negative 1 equals negative 6 over 3 equals negative 2

Practice Problem #4

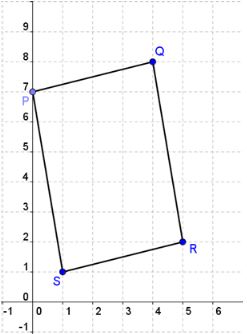
What kind of quadrilateral is PQRS? Justify your answer. P(0, 7), Q(4, 8), R(5, 2), and S(1, 1).

We start this problem by graphing PQRS on the coordinate plane as show in the image. However, we will not be able to identify PQRS by the graph alone. Next, calculate the slope of all of the sides to see if any are parallel. Always use the first point in the segment as (x1, y1) and the second as (x2, y2) for your calculations.
If the lines are parallel, their slopes are equal.

Quadrilateral PQRS with vertices P(0, 7), Q(4, 8), R(5, 2), and S(1, 1).
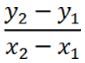
the fraction with numerator y sub 2 minus y sub 1 and denominator x sub 2 minus x sub 1

What is the slope of PQ?

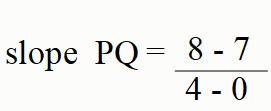
slope of PQ eauals the fraction with numerator 8 minus 7 and denominator 4 minus 0
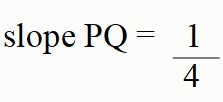
slope of PQ equals one-fourth

What is the slope of Ps?

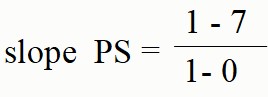
slope of PS equals the fraction with numerator 1 minus 7 and denominator 1 minus 0
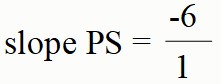
slope of PS equals the fraction with numerator minus 6 and denominator 1

slope PS = -6

What is the slope of QR?

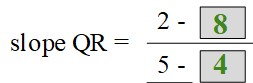
slope of QR equals the fraction with numerator 2 minus 8 and denominator 5 minus 4
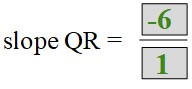
slope of QR equals the fraction with numerator minus 6 and denominator 1

slope QR = -6

What is the slope of RS?

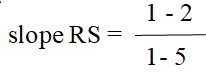
slope of RS equals the fraction with numerator 1 minus 2 minus 8 and denominator 1 minus 5
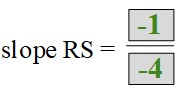
slope of RS equals the fraction with numerator minus 1 and denominator minus 4
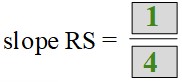
slope of RS equals the fraction with numerator 1 and denominator 4

slope RS = 4

Now that we have determined the slopes, are any sides parallel? Answer: Yes, There are two sets of parallel sides.

Which side is parallel to PQ? Answer: RS

Which side is parallel to PS? Answer: QR

Are there any sides that are perpendicular to one another? Answer: No, and that allows us to limit the type of quadriliateral further.

Now, we must calculate the length of the sides.

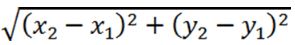
the square root of open paren x sub 2 minus x sub 1 close paren squared plus open paren y sub 2 minus y sub 1 close paren squared

What is the length of PQ?

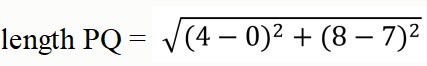
length of PQ equals the square root of open paren 4 minus 0 close paren squared plus open paren 8 minus 7 close paren squared
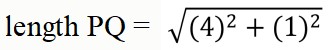
length of PQ equals the square root of open paren 4 close paren squared plus open paren 1 close paren squared
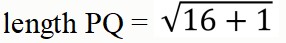
length of PQ equals the square root of 16 plus 1
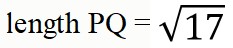
length of PQ equals the square root of 17

What is the length of PS?

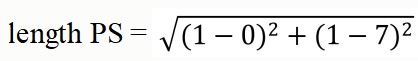
length of PS equals the square root of open paren 1 minus 0 close paren squared plus open paren 1 minus 7 close paren squared
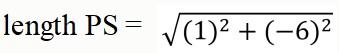
length of PS equals the square root of open paren 1 close paren squared plus open paren minus 6 close paren squared
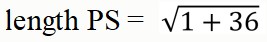
length of PS equals the square root of 1 plus 36
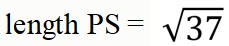
length of PS equals the square root of 37

What is the length of QR?

length of QR equals the square root of open paren 5 minus 4 close paren squared plus open paren 2 minus 8 close paren squared
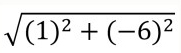
length QR = length of QR equals the square root of open paren 1 close paren squared plus open paren minus 6 close paren squared
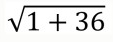
length QR = length of QR equals the square root of 1 plus 36
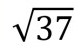
length QR = length of QR equals the square root of 37

What is the length of RS?

length of RS equals the square root of open paren 1 minus 5 close paren squared plus open paren 1 minus 2 close paren squared
length of RS equals the square root of open paren minus 4 close paren squared plus open paren minus 1 close paren squared
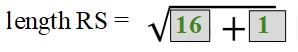
length of RS equals the square root of 16 plus 1
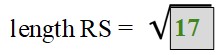
length of RS equals the square root of 17

So we can say that two pairs of sides are congruent. And the anwers to our orignal question, what kind of quadrilateral is PQRS is parallelogram.