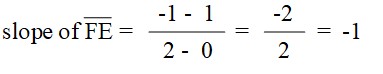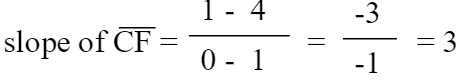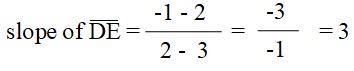Learn
Proving Quadrilaterals are Parallelograms
The last lesson taught you properties of a parallelogram and how to apply them to find missing side lengths and angle measures. This lesson will teach you to use the properties to verify if a quadrilateral is a parallelogram.
To prove a quadrilateral is a parallelogram, the figure must have at least one of these properties.
- Both pairs of opposite sides are parallel
- Both pairs of opposite sides are congruent
- Both pairs of opposite angles are congruent
- Consecutive angles are supplementary
- Diagonals bisect each other
Additional Property
The next property was not given in the last lesson but is also true to prove a quadrilateral is a parallelogram. Add it to your list. If one pair of opposite sides are both parallel and congruent, then the figure is a parallelogram.
Example #1
Is there enough information to prove the quadrilateral is a parallelogram? Explain.
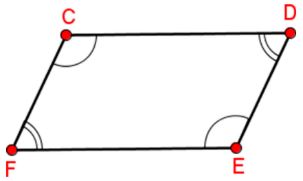
Solution: Use the given information to see if it applies to one of the properties of a parallelogram. In this example, you are given that opposite angles are congruent.
Yes, both pairs of opposite angles are congruent.
Parallelograms on the Coordinate Plane
Terrific. Just remember, not all answers will be yes! We can apply these same properties when the figure is located on a coordinate plane. Below are formulas you used in earlier units that will help to solve these problems on a coordinate plane. Write them down.
Distance = ![]()
Slope = 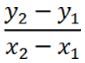
Three Methods
Following are examples showing three methods to prove it is a parallelogram, though there are other as well:
Method 1: Show opposite sides are congruent us the distance formula
Method 2: Show opposite sides are parallel by using the slope formula
Method 3: Show one pair of sides are parallel and congruent by using both the distance and slope formula
Example#2 – Method 1
Open Use coordinate geometry to prove that a given quadrilateral is a parallelogram in a new tab
Example#2 – Method 2
Open Use coordinate geometry to prove that a given quadrilateral is a parallelogram in a new tab
Example#2 – Method 3
Open Use coordinate geometry to prove that a given quadrilateral is a parallelogram in a new tab
Note on Answers
You may use any method to determine whether or not quadrilaterals are parallelograms, but the actual slope or distance must be given in your answer.
Sample Answer: Because both pairs of opposite sides are parallel with slopes of 2 and - ![]() , then ABCD is a parallelogram.
, then ABCD is a parallelogram.
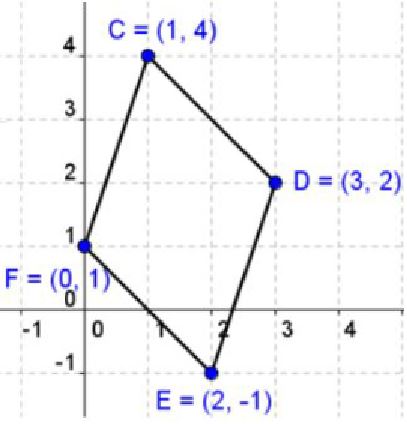
Example #3
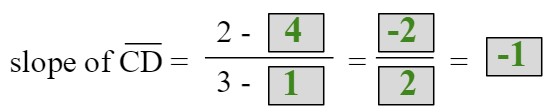
You try one using method 2. Method 2 if to find the slope of the opposite sides wusing the slope formula to see if they are equal.
Show that C(1, 4), D(3, 2), E(2, -1), F(0, 1) are vertices of a parallelogram.