Learn
Parallelograms
A quadrilateral is a polygon that has four sides.
A unique property of polygons you learned in the previous lesson is that the interior angles of a convex quadrilateral have a sum of 360°.
S = 180 °(4 - 2) or S = 360°
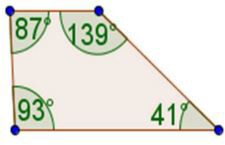
87°+139°+93°+41°=360°
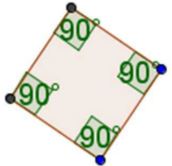
90°+90°+90°+90°=360°
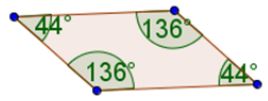
44°+136°+136°+44°=360°
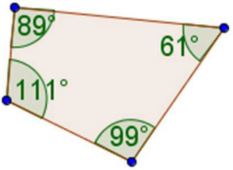
89°+111°+99°+61°=360°
Parallelograms
The first unique quadrilateral that you will learn is parallelogram. The key word in "parallelogram" is parallel.
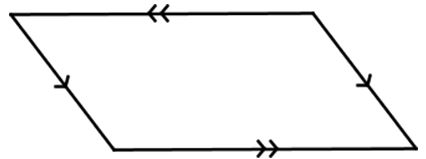
A parallelogram is a quadrilateral in which both pairs of opposite sides are parallel.
Remember that arrow marks are symbols used to identify parallel lines and segments. Matching arrows identify which lines are parallel.
Special Parallelograms
These figures are also parallelograms. Do you know the names of these?
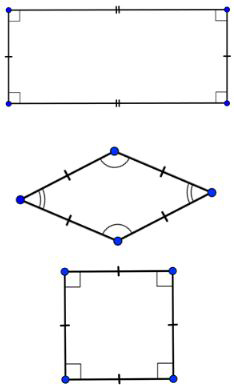
Answer: Rectangle, Rhombus, Square
For this lesson, we will use the shape of the parallelogram on the previous slide because the above parallelograms will be discussed in further detail later in the unit.
Properties - Opposite Sides
The following are properties based on theorems about parallelograms. Write these properties down for future use.
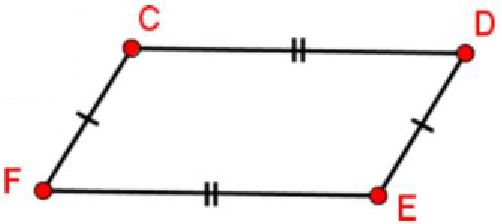
In a parallelogram, opposite sides are congruent.
line CF ≅ line DE
line FE ≅ line CD
Properties - Opposite Angles
In a parallelogram, opposite angles are congruent.
∠c ≅ ∠e
∠f ≅ ∠d
Properties - Consecutive Angles
In a parallelogram, consecutive angles (angles that share a side) are supplementary.
m∠f + m∠e = 180°
m∠e + m∠d = 180°
m∠d + m∠c = 180°
m∠c + m∠ f = 180°
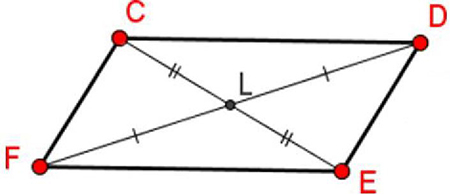
Properties - Diagonals
In a parallelogram, diagonals bisect (divide into two equal sections) each other.
Solving Parallelogram Problems
When solving problems with parallelograms, pay close attention to the given information, such as k = ∠120 in the next example. When the measurement of a line or angle is given, that means you will need that information to solve the parallelogram. To solve the following problem and find ∠L, you needed to know that consecutive angles in a parallelogram are supplementary. This means that any two angles that are connected by a single line segment, like ∠L and ∠k, added together equal 180°. Opposite angles, like ∠L and ∠n, are equal.
Example #1
Open Apply Properties of Parallelograms to Find Unknown Angle Measures in a new tab
Brightstorm: Parallelogram Properties is a video that explains the properties you learned in this lesson along with how to solve problems similar to the previous problems we covered. Problem 3 is an excellent example to help you solve task problems that involve two variables.