Learn

Polygons

As we begin the lesson on polygons, we must first understand the vocabulary used with two-dimensional figures.

We will then study in depth the polygon with the least number of sides possible in order to understand the properties of polygons with more sides.

Vocabulary

  • polygon
  • vertex
  • side
  • diagonal
  • convex
  • concave
  • n-gon
  • equilateral polygon
  • equiangular polygon

A polygon is a closed figure with a finite number of sides which are line segments.

polygon

An angle formed by the intersection of two sides is called a vertex of the polygon.

A polygon has to meet the following three criteria:

  • a polygon must have at least three sides
  • all sides must be line segments
  • each side intersects exactly two other sides, one at each endpoint

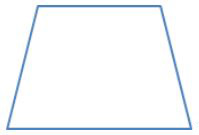
Not Polygons

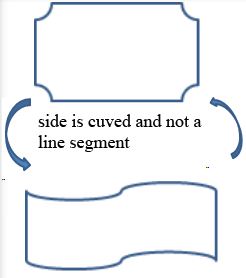
two examples of figures that are not polygrams because they have sides that are curved

 

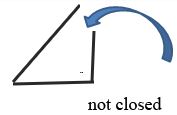
a figure that is not a polygon because it has a non closed section

 

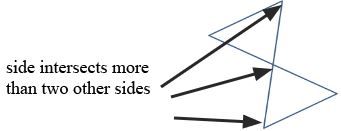
a figure that is not a polygon because it has sides that intersect more than two other sides

Parts of a Polygon

Below is an example of a polygon. Remember each endpoint is called a vertex. Plural for vertex is vertices. We would say this polygon has four vertices. You name a polygon by listing the vertices consecutively. It does not matter which endpoint you start with or if you go clockwise or counterclockwise rotation. We could name the polygon above as polygon ABCD or ADCB and still be correct.

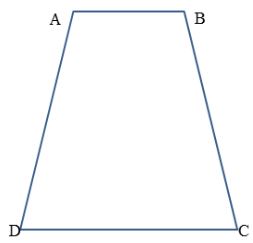
Polygon with point A in upper left corner, point B in upper right corner, point C lower right corner and point D lower left corner

Convex Polygons

Diagonals are helpful in determining if a polygon is convex or concave. A polygon is considered convex if none of the diagonals of the polygon are outside of the figure.

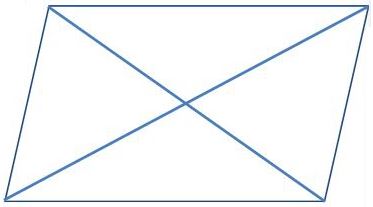
convex polygon

Concave Polygons

A polygon is classified as concave if at least one diagonal is outside of the polygon. Notice how diagonal AB is outside of the polygon, thus concave.

concave polygon

Convex or Concave

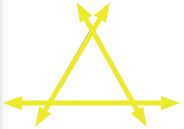
OPTIONAL way to determine if a polygons are convex or concave: To check, extend the lines containing each side. If any of the lines contain any point in the interior of the polygon, then it is concave. Otherwise it is convex. The triangle below is convex, while the pentagon is concave.

triangle with lines extending pass the figure showing it is convex

 

rectangle with lines extending pass the figure showing it is concave

Exercise #1

Identify if the polygons are conves or concave.

hexagon Answer: concave

An octagon

Answer: Convex

A right triangle

Answer: Convex

A pentagon

Answer: Convex

A classical star

Answer: Concave

An arrow made from a triangle attached to the end of a rectangle

Answer: Concave

Names of Polygons

You name a polygon by the number of sides it contains. Use the chart below.

# of sides Name
3 triangle
4 quadrilateral
5 pentagon
6 hexagon
7 heptagon
8 octagon
9 nonagon
10 decagon
11 hendecagon
12 dodecagon
n sides n-gon

n-gon

Notice the last row has "n" sides. This is primarily used for polygons when the number of sides are greater than 12.

Replace the "n" with the number of sides.

For instance, a polygon with 13 sides would be called a 13-gon.

What would a polygon with 46 sides be called?

Answer: 46-gon

Exercise #2

Identify the polygons by name.

A polygon with 5 sides

Answer: pentagon

A polygon with 10 sides

Answer: decagon

An arrow shape with 7 sides

Answer: heptagon

A polygon with 8 sides

Answer: octagon

A 4 sided figure with slanted sides

Answer: quadrilateral

Equilateral and Equiangular

We can also identify a polygon as:

equilateral - all sides congruent

An 8 sided figure with all equal length sides

equiangular - all angles are congruent

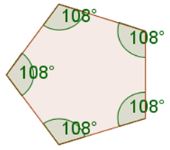
A 5 sided figure with each vertice havig 108 degree angle

Regular Polygons

If a figure has all sides congruent and all angles congruent then it is called a regular polygon.

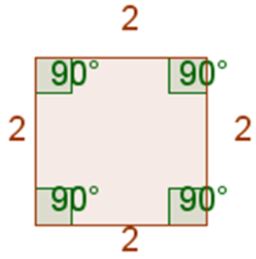
A quadrilateral with all 90 degree angles and all side lengths of 2

A square is a regular quadrilateral because all four sides are congruent and all four angles are congruent.

Classify Polygons

You can now:

  • Classify a polygon as convex or concave
  • Name the polygon by the number of sides
  • Identify if the polygon is equilateral, equiangular or both - thus regular or neither

Try This One

Classify this polygon:

A figure with 6 sides, but one of the angles is greater than 180 degrees

Is it concave or convex?

Answer: Concave

What is the name of this polygon?

Answer: hexagon

Is it equilateral, equiangular, both, or neither?

Answer: neither

Classify Polygons

Look at the figure and see if you can decide who is correct in classifying the polygon.

A figure with 4 sides with 4 right angles. The top length is 4.2 and the right side length is 4.1

Chase said convex, regular, quadrilateral.

Anna said convex, equiangular, quadrilateral.

Who is correct and why?

Answer: Anna; The sides are not congruent so it is not regular. Anna is correct.

 

Vertices of a Polygon Given Lines

Draw a Polygon a Coordinate Plane

To draw a polygon in the coordinate plane given the coordinates of its vertices, first plot the ordered pairs. Then, connect the order pairs with line segments.

A blank coordinate plane that goes from -7 to 7 on the x-axis and -7 to 7 on the y-axis.

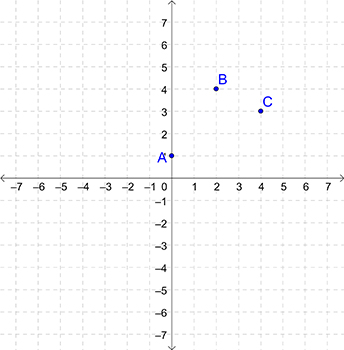
For example, to draw a triangle with coordinates A(0,1), B(2,4) and C(4,3) on the coordinate plane, you will first plot the points A(0,1), B(2,4) and C(4,3) on the coordinate plane.

The points A(0,1), B(2,4), and C(4,3) on a coordinate plane.

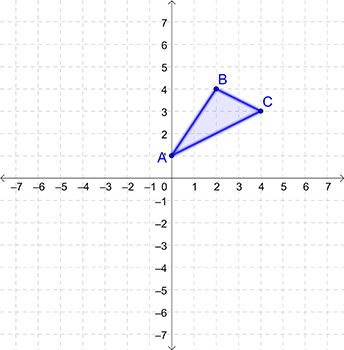
Then, connect the points with line segments.

A 3-sided polygon on a coordinate plane. The coordinates of the vertices are A(0,1), B(2,4), C(4,3).

Vertices of a Polygon Given Lines

The vertices of a polygon in a coordinate plane are the points of intersection of the lines that contain the sides of the polygon.

Early in the lesson, you have learned that the vertex of a polygon is where two sides meet or intersect.

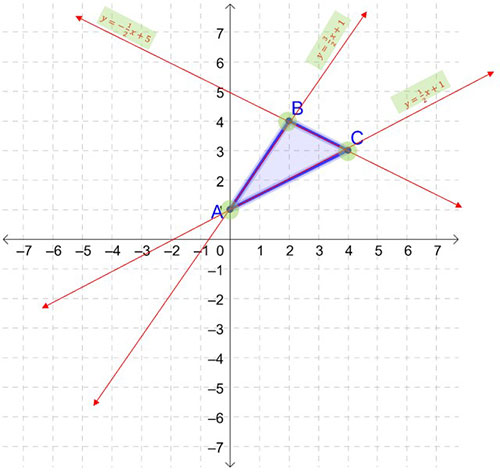
A 3-sided polygon on a coordinate plane. The coordinates of the vertices are A(0,1), B(2,4), C(4,3). Three lines, y = (3/2)x + 1, y = (1/2)x + 1, and y = -(1/2)x + 5, are drawn through the sides of the polygon.

If you are given the equations of the lines that form a polygon in a coordinate plane, you can find the coordinates of the vertices by finding the points of intersection of the lines.

The points of intersection of the lines in the diagram are (0,1), (2,4), and (4,3). So, the vertices of the triangle that is formed by the three lines are (0,1), (2,4), and (4,3).

How to Find the Point of Intersection

The point of intersection of two non-parallel lines can be found by:

Method 1:

  1. Rewrite the equations of the lines in slope-intercept form (Solve each equation for y).
  2. Set the two expressions for y equal to each other.
  3. Solve for the value of the x variable. The value of the x variable is the x-coordinate of the point of intersection.
  4. Solve for the value of the variable y by substituting the value of the x variable into either of the original equations of the lines. The value of the y variable is the y-coordinate of the point of intersection.

Method 2:

  1. Graph each equation on the coordinate plane.
  2. Locate the points of intersection on the graph.

Example #5 Method 1 - Part 1

Find the coordinates of the vertices of the triangle formed by the lines: y = 3x − 8, y = -x + 4, and y = x + 2.

First, find the intersection of the lines: y = 3x − 8 and y = -x + 4.

Step 1: Write the equations of the lines in slope-intercept form (Solve each equation for y).

  • Answer: The equations are already in slope-intercept form.

Step 2: Set the two expressions for y equal to each other.

  • Answer: 3x − 8 = -x + 4

Step 3: Solve for the value of the x variable. The value of the x variable is the x-coordinate of the point of intersection.

3x minus 8 equals negative x plus 4. Add x to both sides, you have 4x minus 8 equals 4. Add 8 to both sides, you have 4x over 4 equals 12 over 4. Simplify both sides. You got x equals 3.

Step 4: Solve for the value of the variable y by substituting the value of the x variable into either of the original equations of the lines. The value of the y variable is the y-coordinate of the point of intersection.

Substitute x = 3 into the first equation, y = 3x − 8.

y = 3x − 8

y = 3(3) − 8

y = 9 − 8

y = 1

 

So, the point of intersection of the lines, y = 3x − 8 and y = -x + 4, is (3,1).

Example #5 Method 1 - Part 2

Now, find the intersection of the lines: y = 3x − 8 and y = x + 2.

Step 1: Write the equations of the lines in slope-intercept form (Solve each equation for y).

  • Answer: The equations are already in slope-intercept form.

Step 2: Set the two expressions for y equal to each other.

  • Answer: 3x − 8 = x + 2

Step 3: Solve for the value of the x variable. The value of the x variable is the x-coordinate of the point of intersection.

3x minus 8 equals x plus 2. Add negative x to both sides, you have 2x minus 8 equals 2. Add 8 to both sides, you have 2x over 2 equals 10 over 2. Simplify both sides. You got x equals 5.

Step 4: Solve for the value of the variable y by substituting the value of the x variable into either of the original equations of the lines. The value of the y variable is the y-coordinate of the point of intersection.

Substitute x = 5 into the first equation, y = 3x − 8.

y = 3x − 8

y = 3(5) − 8

y = 15 − 8

y = 7

 

So, the point of intersection of the lines, y = 3x − 8 and y = x + 2, is (5,7).

Example #5 Method 1 - Part 3

Now, find the intersection of the lines: y = -x + 4 and y = x + 2.

Step 1: Write the equations of the lines in slope-intercept form (Solve each equation for y).

  • Answer: The equations are already in slope-intercept form.

Step 2: Set the two expressions for y equal to each other.

  • Answer: -x + 4 = x + 2

Step 3: Solve for the value of the x variable. The value of the x variable is the x-coordinate of the point of intersection.

negative x plus 4 equals x plus 2. Add x to both sides, you have 4 equals 2x plus 2. Add negative 2 to both sides, you have two halves equals 2 x over 2. Simplify both sides. You got x equals 1.

Step 4: Solve for the value of the variable y by substituting the value of the x variable into either of the original equations of the lines. The value of the y variable is the y-coordinate of the point of intersection.

y = -x + 4

y = −(1) + 4

y = 3

 

So, the point of intersection of the lines, y = -x + 4 and y = x + 2, is (1,3).

Example #5 Method 1 - Solution

Solution:

  • The point of intersection of the lines: y = 3x − 8 and y = -x + 4 is (3,1).
  • The point of intersection of the lines: y = 3x − 8 and y = x + 2 is (5,7).
  • The point of intersection of the lines: y = -x + 4 and y = x + 2 is (1,3).

The coordinates of the points (3,1), (5,7), and (1,3) represent the vertices of the triangle that are formed by the lines: y = 3x − 8, y = -x + 4, and y = x + 2.

So, the vertices of the triangle are (3,1), (5,7), and (1,3).

Example #6 Method 2

Watch Find the Coordinates of the Vertices of a Polygon Formed by Lines.

Go to Find the Vertices of a Polygon Given Lines if you would like to practice along with this video.

Open Find the Coordinates of the Vertices of a Polygon Formed by Lines in a new window

Note: The presentation may take a moment to load.