Learn
Congruent Triangles - SSS and SAS
SSS Congruence
When two triangles are congruent, all corresponding sides and angles are congruent.
It is obvious that these two figures are the same size when all the information is given.
There are six corresponding congruent statements because each triangle has six parts.
Three Angles:
- ∠A ≅ ∠X
- ∠B ≅ ∠Y
- ∠C ≅ ∠Z
Three Sides:
- segment BC ≅ segment YZ
- segment AC ≅ segment XZ
- segment AB ≅ segment XY
This lesson will focus on proving that two triangles are congruent by using shortcut methods.
Sometimes you may not know all the information about two different triangles but they may look congruent. Look at the triangles here.
Just because two of the sides are equal does not necessarily mean the triangles are congruent.
SSS Congruence
There are methods you will learn that may show two triangles are congruent even though all the information about the angles and sides may not be given.
The first method is called the SSS Congruence Postulate. The postulate states: If three sides of one triangle are congruent to three sides of another, then the triangles are congruent.
SSS Example
Let's look at an example using the SSS postulate.
Example: List the corresponding congruent parts of the triangles. Is this enough information to prove the triangles are congruent? If so, write the congruence statement and the method used to prove they are congruent.
Solution: First we will list all given corresponding congruent parts.
segment AB ≅ segment FE
segment AC ≅ segment FD
segment BC ≅ segment ED
Now we have enough information to state the triangles are congruent. When writing the following congruence statement, the corresponding vertices must be in the same location:
Yes, △ABC ≅ △FED by SSS postulate.
Proof Using Prior Knowledge
Sometimes information is not given with congruent symbols. You must use prior knowledge to determine that sides and angles are congruent.
The Math Warehouse has an example of this concept.
Scroll past Example 1 to A Side by Side Proof.
Click the Next icon to reveal the information in the two column proof.
Example #1
Open Prove That Two Triangles Are Congruent Using SSS Congruence Postulate in a new tab
Application
Rigid Motions
Recall the transformations used in prior lessons.
Reflection is a flip
Rotation is a turn
Translation is a slide
Dilation is a scale
Which transformation does not hold congruence?
- Reflection
- Rotation
- Translation
- Dilation
Answer: Dilation; See the change in size? These figures are not congruent. It would not be the others because they are the same size, so they do not hold congruence.
Example #2
Open Prove Triangles Are Congruent Using SSS Congruence Postulate in a new tab
SAS Congruence
Included Angle
Great, you have just learned one method to prove two triangles are congruent.
Before we move on to the next method, let's go over a concept that you will need to learn to better understand the SAS postulate.
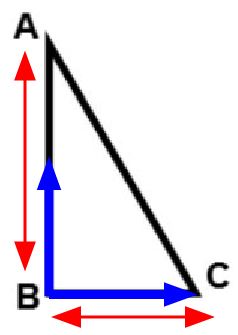
An included angle is the angle that is formed by two sides. In the diagram, the included angle formed by the sides AB and BC is ∠B because that is where the two sides intersect.
Example #3
Let's see if you can identify included angles.
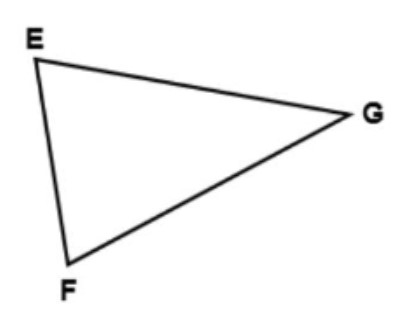
What is the included angle formed by the sides segment EG and segment FG? ∠___
Answer: ∠G
Example #4
What is the included angle formed by the sides segment XY and segment XZ?
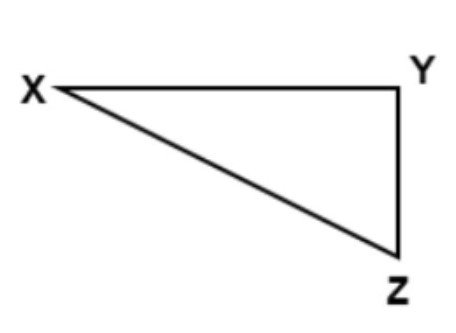
Answer: ∠X
SAS Postulate
Terrific, now that you can identify an included angle, you can use the next method to prove triangles are congruent.
The SAS Postulate states that if two sides and an included angle of one triangle are congruent to two sides and an included angle of a second triangle, then the triangles are congruent.
Examples and Practice
For examples and interactive practice using the SAS Postulate, go to Math Warehouse.
If you would like to see a video of someone explaining these concepts along with solving problems go to Brightstorm: SSS and SAS.
Example #5
Open Prove That Two Triangles Are Congruent Using SAS Congruence Postulate in a new tab