6.03 Triangle Perimeter and Area in the Coordinate Plane

Learn

Distance Formula Review

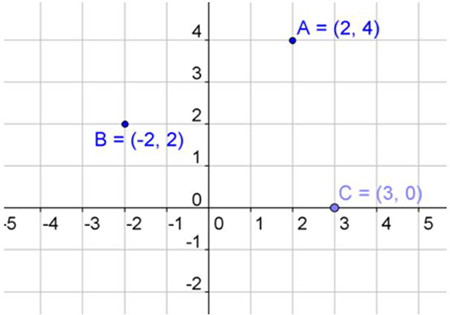
Review Ordered Pairs

Remember that an ordered pair is represented as (x, y). The x tells you how many steps right or left. The y tells you how many steps up or down before placing the dot for the point.

Three Points A, B, and C on a coordinate plane. The coordinates of A, B, and C are A(2,4) and B(negative 2, 2), and C(3,0).

Distance Formula Review

Also remember you can find the distance of the line segment AB by using the distance formula.

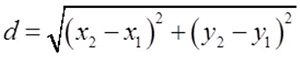
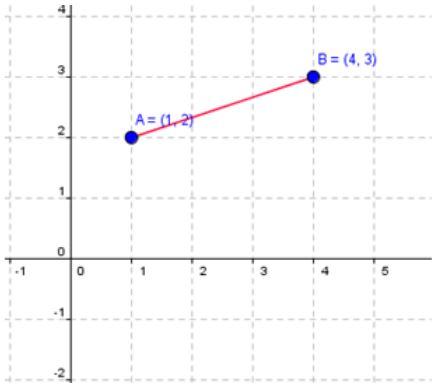
Segment AB on a coordinate plane. The coordinates of A and B are A(1,2) and B(4,3).

Remember to label the points. One point we will label (x₁ , y₁) and the other point will be labeled (x₂, y₂). It does not matter which point you label point one. For our example we will label (1, 2) as (x₁ , y₁) and (4, 3) as (x₂ , y₂). The rest is just placing the values into the correct location of the formula.

Start by rewriting your distance formula.

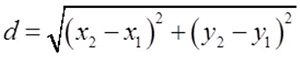
Substitute in your values.

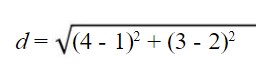
d equals the square root of open paren 4 minus 1 close paren squared plus open paren 3 minus 2 close paren squared

Simplify parentheses.

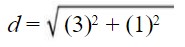
d equals the square root of 3 squared plus 1 squared

Apply the exponents.

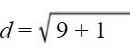
Simplify by adding.

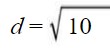
d = 3.2
Calculate the value of the square root of 10 using a calculator.

Example #1

Open Apply the Distance Formula to Find the Distance between Two Points Given Their Coordinates in a new tab

Landscape Designs

Perimeter

Recall that the perimeter is the sum of all the sides of the polygon. We will look at finding the perimeter of a triangle given the coordinates of the vertices.

Vocabulary

Perimeter
Distance Formula

Example #2

Open Find the Perimeter of a Triangle in a Coordinate Plane in a new tab

Landscape Design

A couple wants to plant flowers in a triangular area. They ask a landscape architect to help. The architect will take the layout of the land and desires of the customer to make a drawing for the customer to see the final outcome on paper before actually beginning the hands on portion of the project.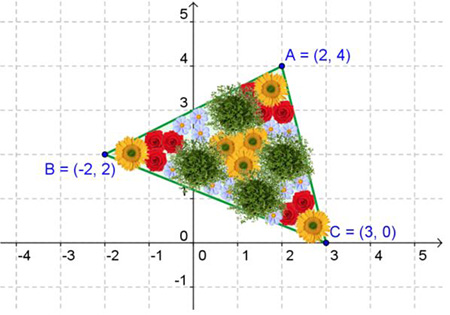 A triangle in a coordinate plane. The vertices of the triangle are A(2,4) , B(negative 2, 2), and C(3,0).

Take this drawing for example. They decide to make a border around the edges with 6 inch stones. In order to find the number of stones, they must determine the distance around the triangle - known as the perimeter! We will come back to this example after a quick review.

Example #3

Open Find the Perimeter of a Triangle on the Coordinate Plane Using the Distance Formula in a new tab

Triangle Area in the Coordinate Plane

Perimeter

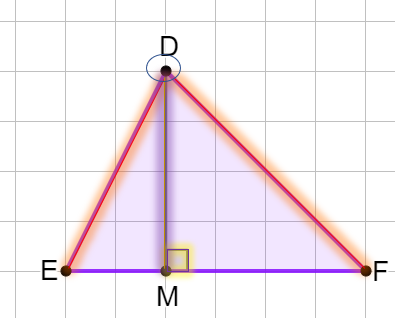
Any side of a triangle can be considered the base of the triangle. Let’s let segment EF be the base of ∆DEF. The height of a triangle is the perpendicular segment that is drawn from the base of the triangle or a line containing the base to the vertex that is opposite that base. The height and the base of a triangle are perpendicular to each other. Segment DM is the height of ∆DEF, because it the perpendicular segment that is drawn from the base, segment EF ,to the vertex, point D, that is opposite that base.

Formula

The formula for finding the area of a triangle is A = 1/2 bh where b is the length of the base and h is the length of height of the triangle.

Example #4

To find the area of ∆DEF, first find the lengths of the base and the height of the triangle. In the diagram, segment EF is the base and segment DM is the height of the triangle.

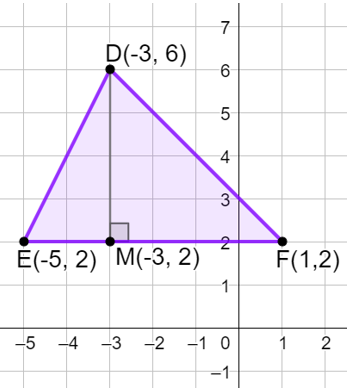
Step 1: Find the length of the base, segment EF. Segment EF is a horizontal segment. To find the length of a horizontal segment on a coordinate plane it best to calculate the absolute value of the difference of the x-coordinates of its endpoints. So, EF is the absolute value of the difference of the x-coordinates of E(-5, 2) and F(1, 2). EF = |-5-1| = |-6| = 6. The length of the base is 6 units.
Step 2: Find the length of the height, segment DM. Segment DM is a vertical segment. To find the length of a vertical segment on a coordinate plane it best to calculate the absolute value of the difference of the y-coordinates of its endpoints. So, DM is the absolute value of the difference of the y-coordinates of D(-3, 6) and M(-3, 2). DM = |6-2| = |4| = 4. The length of the height is 4 units.
Step 3: Find the area. Write the formula for finding the area of a triangle.
A = ½ bh The length of the base is EF and the length of the height is DM.
A = ½ (EF)(DM)
Next substitute in 6 units for EF and 4 units for DM.
A = ½ (6 units)(4 units)
Simplify. Multiply ½ (6 units).
A = (3 units)(4 units)
Simplify. Multiply (3 units) (4 units).
A = 12 units₂

Example #5

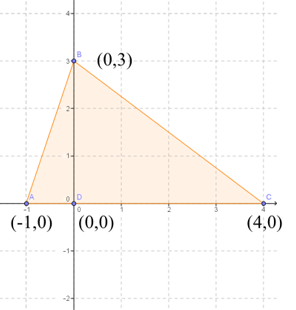
To find the area of ∆ABC, first find the lengths of the base and the height of the triangle. In the diagram, AC is the base and BD is the height of the triangle.

Step 1: Find the length of the base, segment AC. Segment AC is a horizontal segment. To find the length of a horizontal segment on a coordinate plane it best to calculate the absolute value of the difference of the x-coordinates of its endpoints. So, AC is the absolute value of the difference of the x-coordinates of A(-1, 0) and C(4, 2).
AC = |-1-4| = |-5| = 5. The length of the base is 5 units.
Step 2: Find the length of the height, segment BD. Segment BD is a vertical segment. To find the length of a vertical segment on a coordinate plane it best to calculate the absolute value of the difference of the y-coordinates of its endpoints. So, BD is the absolute value of the difference of the y-coordinates of B(0, 3) and D(0, 0). BD = |3-0| = |3| = 3. The length of the height is 3 units.
Step 3: Find the area. Write the formula for finding the area of a triangle.
A = ½ bh
The length of the base is EF and the length of the height is DM.
A = ½ (AC)(BD)
Next substitute in 5 units for AC and 3 units for BD.
A = ½ (5 units)(3 units)
Simplify. Multiply ½ (7 units).
A = (2.5 units)(3 units)
Simplify. Multiply (2.5 units) (3 units).
A = 7.5 units₂

← Back