Learn
Triangle Classification and Angle Theorems
Remember that in the previous lesson we learned that the polygon with the smallest number of sides is called a triangle. We will begin our in-depth study of the triangle
Vocabulary
- triangle
- interior angle
- exterior angle
- scalene triangle
- isosceles triangle
- equilateral triangle
- acute triangle
- obtuse triangle
- right triangle
- equiangular triangle
Classify Triangles by Sides
We know that a triangle has three sides. Remember congruent ≅ means equal in measure!
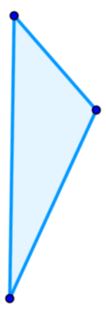
Scalene Triangle - no sides congruent
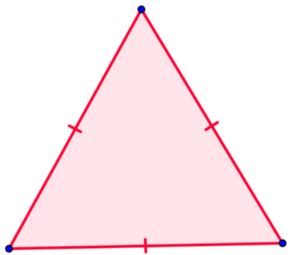
Equilateral Triangle - all three sides congruent
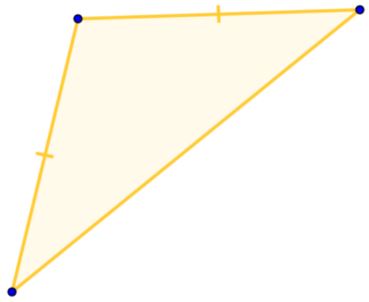
Equilateral Triangle - at least two sides congruent
Complete the activity GeoGebra: Types of triangles by sides to find out more about types of triangles, their sides, and angles.
Exercise #1
Open Classify Triangles by Their Side Lengths in a new tab
Algebraic Expressions
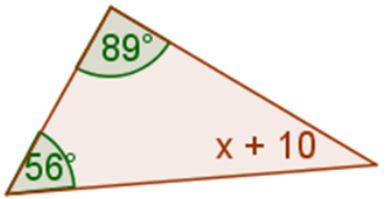
Sometimes the angles are written as algebraic expressions with more than one term. You would still write the equation = 180° then solve. (x + 10) + 56° + 89° = 180° or x + 10 + 56° + 89° = 180°
Recall Angle Measures
m∠A is read as the measure of angle A
Acute Angle - measures less than 90°
Right Angle - measures 90°
Obtuse Angle - measures more than 90° but less than 180°
Triangle Angles
acute triangle - three acute angles
equiangular triangle - three acute angles of 60° each
obtuse triangle - one obtuse angle
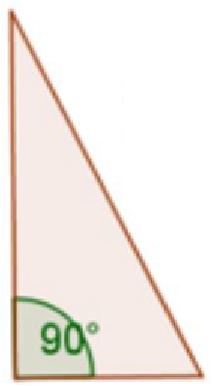
right triangle - one right angle
Acute Versus Equiangular
Note that an equiangular triangle is also known as acute. Just in this case, all three angles are ≅. Since equiangular is more descriptive, we say it is equiangular.
Scalene Triangle - no sides congruent; Equilateral triangle - all three sides congruent.
Exercies #2
Open Classify Triangles by Their Angle Measures in a new tab
Exercies #3
Open Equilateral and Equiangular Triangles in a new tab
Exercies #4
Open Classify Triangles by Their Angle Measures and Side Lengths in a new tab
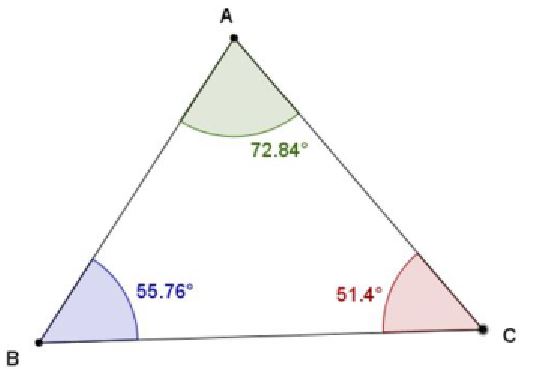
Sum of Interior Angles of a Triangle
m∠A + m∠B = m∠C = 180°
Why? Because the angle measurements form a straight line and the measurement of a straight angle is 180°. Complete this GeoGebra: ACCESS – Sum of Angles in Triangle activity to see if the sum changes if you change the shape of the triangle.
Triangle Sum Theorem
Given any ∠ABC, the sum of the interior angles = 180°.
Exercies #5
Open Apply the Triangle Sum Theorem to Find Unknown Values in a new tab
Exterior Angles
Let’s look at another theorem in Geometry that is Triangle Classification and Angle Theorems le is formed as shown below.
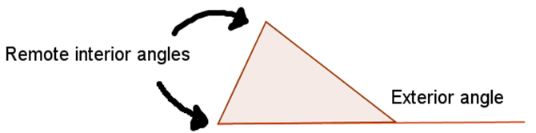
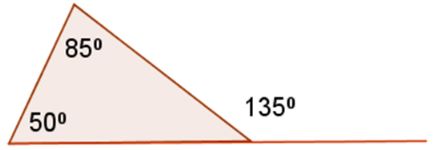
Exterior Angle Theorem
The Exterior Angle Theorem states that the exterior angle is equal to sum of the two remote interior angles.
Exercies #6
Open Prove the Exterior Angle Theorem in a new tab
Exercies #7
Open Apply the Triangle Exterior Angle Theorem to Find Unknown Angle Measures in a new tab