Learn
Proving Lines Parallel
In the last lesson we learned relationships about certain pairs of angles when two parallel lines are cut by a transversal.
This lesson is similar, except we will not be given that the two lines are parallel but instead we will be asked to prove if the two lines are parallel or not parallel based on information that is provided.
Alternate Exterior Angles Converse Theorem
First, let's look at information that will help us determine if the lines are parallel. We are going to use the converse of the theorems we learned from the lsat lesson.
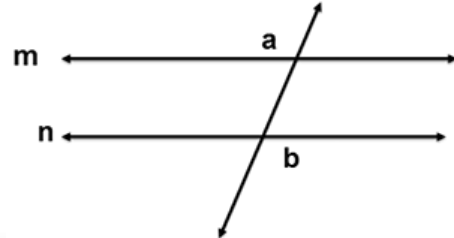
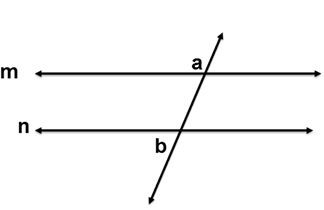
Alternate Exterior Angles Converse Theorem states that if two lines are cut by a transversal and the alternate exterior angles are congruent, then the two lines are parallel.
If ∠a ≅ ∠b then m||n
Alternate Interior Angles Converse Theorem
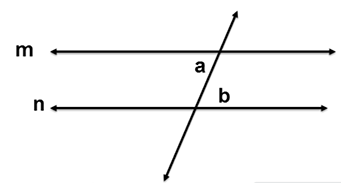
Alternate Interior Angles Converse Theorem states that if two lines are cut by a transversal and the alternate interior angles are congruent, then the two lines are parallel.
If ∠a ≅ ∠b then m||n.
Corresponding Angles Converse Theorem
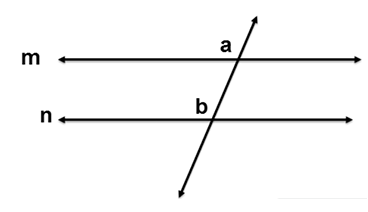
Corresponding Angles Converse Theorem states that if two lines are cut by a transversal and the corresponding angles are congruent, then the two lines are parallel.
If ∠a ≅ ∠b then m||n.
Remember that if the
- alternate interior angles
- alternate exterior angles
- corresponding angles
are congruent, then the two lines are parallel.
Also, if the following angles are supplementary, then the two lines are parallel.
- Same side interior
- Same side exterior
These are all converse theorems from the last lesson. Have these written in your notes.
Same Side Interior Angles Converse Theorem
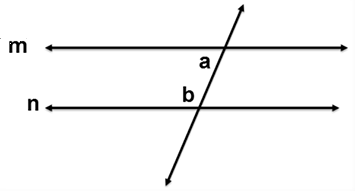
Same Side Interior Angles Converse Theorem states that if two lines are cut by a transversal and the same side interior angles are supplementary, then the two lines are parallel.
If ∠a is supplemetary to ∠b then m||n
Same Side Exterior Angles Converse Theorem
Same Side Exterior Angles Converse Theorem states that if two lines are cut by a transversal and the same side exterior angles are supplementary, then the two lines are parallel.
If ∠a is supplemetary to ∠b then m||n
Example #1
Open Determine If Two Lines Are Parallel Given the Measures of Two Angles in a new tab
Example #2
Open Solve for an Unknown Value That Will Make Two Given Lines Be Parallel in a new tab