Try It

Parallel Lines Practice

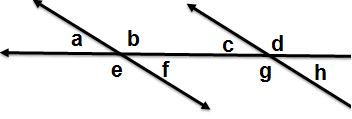
Questions 1 -3 refer to this image.

a transversal intersecting two lines; the transversal forms vertical angles a and d and vertical angles c and b with the first line; the transversal forms vertical angles e and h and vertical angles g and f with the second line
  1. Which angle forms an alternate exterior angle pair with angle b?
    1. d
    2. f
    3. g
    4. e

    Answer: c. The correct answer is g.
    Angles b and g are alternate exterior angles because the angles are outside the parallel lines, and on opposite sides of the transversal. Angles a and h form the other alternate exterior angle pair in this diagram.

  2. Angle h corresponds to angle _____.
    1. g
    2. a
    3. d
    4. f

    Answer: c. The correct answer is d.
    Other corresponding angle pairs in the diagram are: a and e; b and f; c and g.

  3. Which angle forms a same side interior angle pair with angle e?
    1. c
    2. b
    3. h
    4. e

    Answer: a. The correct answer is c.
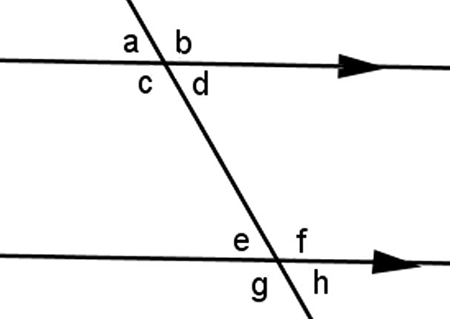
    Angles c and e form a same side interior angle pair because they are inside the parallel lines and on the same side of the transversal. Angles d and f form the other same side interior angle pair in this diagram.

    4. Questions 4 - 6 refer to this image.

    a transversal intersecting two lines; the transversal forms vertical angles a and f and vertical angles e and b with the first line; the transversal forms vertical angles c and h and vertical angles g and d with the second line
  4. Use the diagram to identify the pair of angles e and h.
    1. same side exterior
    2. same side interior
    3. alternate interior
    4. alternate exterior

    Answer: a. same side exterior

  5. Use the diagram to identify the pair of angles f and h.
    1. corresponding
    2. same side interior
    3. alternate interior
    4. alternate exterior

    Answer: a. corresponding

  6. Use the diagram to identify the pair of angles b and g.
    1. corresponding
    2. same side exterior
    3. alternate interior
    4. alternate exterior

    Answer: c. alternate interior

  7. __________ are created where a transversal crosses two (usually parallel) lines. Each pair of these angles are inside the parallel lines, and opposite sides of the transversal.
    1. Same side interior
    2. Alternate exterior
    3. Alternate interior
    4. Same side exterior

    Answer: c. Alternate interior

  8. Angle pair created where a transversal crosses two (usually parallel) lines. Each pair of these angles are outside the parallel lines, and on the same side of the transversal.
    1. same side interior angles
    2. same side exterior angles
    3. alternate interior angle
    4. alternate exterior angle

    Answer: d. alternate exterior angle

  9. Angle pair created where a transversal crosses other (usually parallel) lines. These angles are the ones at the same location at each intersection.
    1. corresponding
    2. alternate exterior
    3. alternate interior
    4. vertical

    Answer: a. corresponding

  10. Angle pair created where a transversal crosses two (usually parallel) lines. Each pair of these angles are outside the parallel lines, and on opposite sides of the transversal.
    1. same side interior
    2. same side exterior
    3. alternate interior angles
    4. alternate exterior angles

    Answer: d. alternate exterior angles

  11. Angle pair created where a transversal crosses two (usually parallel) lines. Each pair of these angles are inside the parallel lines, and on the same side of the transversal.
    1. same side interior
    2. same side exterior
    3. alternate interior
    4. corresponding

    Answer: a. same side interior

  12. Alternate exterior angles, alternate interior angles, vertical angles, and corresponding angles all have what type of angle relationships?
    1. congruent
    2. supplementary

    Answer: a. congruent

  13. Same side interior, same side exterior, and linear pair angles all have what type of angle relationships?
    1. congruent
    2. supplementary

    Answer: b. supplementary