Learn

Parallel Lines Cut by a Transversal

It is amazing how you can find the measures of the angles of intersecting lines given only one angle when the lines are parallel.

Vocabulary

  • transversal interior angles
  • exterior angles
  • corresponding angles
  • alternate interior
  • alternate exterior
  • same side interior
  • same side exterior

Transversal

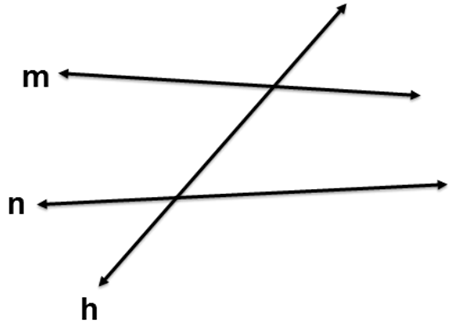
A transversal is a line that intersects two or more lines. Notice below how line h is the transversal because it intersects lines m and n.

Line h intersecting two non-parallel lines m and n

Angles Formed

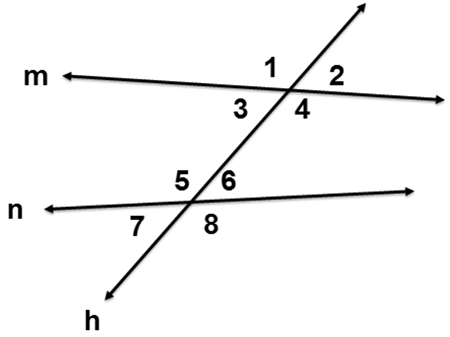
Also, notice the 8 angles that are formed when a transversal intersects two lines.

Line h intersecting lines m and n; lines h and m form vertical angles 1 and 4 and vertical angles 3 and 2; lines h and n form vertical angles 5 and 8 and vertical angles 6 and 7

Parallel Lines Cut by Transversal

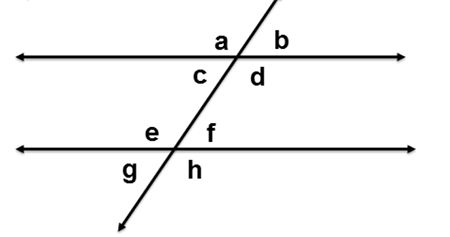
Something unique happens when parallel lines are intersected by a transveral. Certain pair of angles are congruent while other pairs are supplementary. Below are a pair of parallel lines cut by a transversal. Can you identify which angles are congruent and which ones are supplementary?

a transversal intersecting two lines, the transversal forms vertical angles a and d and vertical angles c and b with the first line; the transversal forms vertical angles e and h and vertical angles g and f with the second line

Exercise #1

Can you identify which angles are congruent to ∠a?

a transversal intersecting two lines, the transversal forms vertical angles a and d and vertical angles c and b with the first line; the transversal forms vertical angles e and h and vertical angles g and f with the second line

Exercise #2

Can you identify which angles are supplementary to ∠a?

a transversal intersecting two lines, the transversal forms vertical angles a and d and vertical angles c and b with the first line; the transversal forms vertical angles e and h and vertical angles g and f with the second line

 

Congruent Angles

Write the information below in your notes for future reference.

Below are the pairs of angles that are congruent to each other when two parallel lines are intersected by a transversal.

Alternate interior angles

a transversal intersecting two lines; the transversal forms vertical angles a and d and vertical angles c and b with the first line; the transversal forms vertical angles e and h and vertical angles g and f with the second line; showing angles c and f to be alternate interior angles and angles e and d to be alternate interior angles

Alternate exterior angles

a transversal intersecting two lines, the transversal forms vertical angles a and d and vertical angles c and b with the first line; the transversal forms vertical angles e and h and vertical angles g and f with the second line; showing angles a and h to be alternate exterior angles and angles b and g to be alternate exterior angles

Corresponding angles

a transversal intersecting two lines; the transversal forms vertical angles a and d and vertical angles c and b with the first line; the transversal forms vertical angles e and h and vertical angles g and f with the second line; showing angles a and e to be corresponding angles; showing angles c and g to be corresponding angles; showing angles b and f to be corresponding angles; showing angles d and h to be corresponding angles

Supplementary Angles

Write the information below in your notes for future reference.

Below are the pairs of angles that are supplementary to each other when two parallel lines are intersected by a transversal.

Same side interior angles

a transversal intersecting two lines; the transversal forms vertical angles a and d and vertical angles c and b with the first line; the transversal forms vertical angles e and h and vertical angles g and f with the second line; showing angles c and e to be same-side interior angles; showing angles d and f to be same-side interior angles

Same side exterior angles

a transversal intersecting two lines; the transversal forms vertical angles a and d and vertical angles c and b with the first line; the transversal forms vertical angles e and h and vertical angles g and f with the second line; showing angles a and g to be same-side exterior angles; showing angles b and h to be same-side exterior angles

 

Interactive Diagrams

Each link below allows you to move lines to see how this affects each pair of angles. Also, make sure you click "other pair" to the right of the diagram to see all pairs of each set.

Explore more with GeoGebra.

Angle Measures

Now that you can identify each pair of angles, let's apply this information to solve problems. If we know just one angle measure then we can find the other seven angle measures when the two parallel lines are intersected by a transversal.

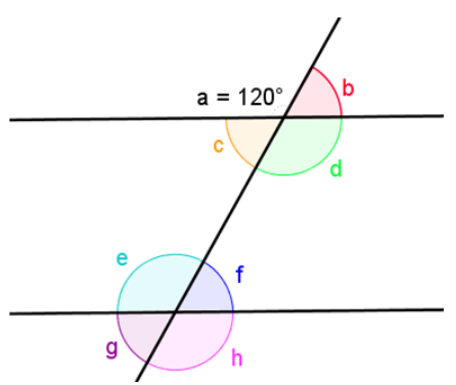
a transversal intersecting two lines; the transversal forms vertical angles a and d and vertical angles c and b with the first line; the transversal forms vertical angles e and h and vertical angles g and f with the second line; the measure of angle a is given as 120 degrees

This is how each angle relates to angle a:

  • ∠a and ∠b form a linear pair, so they sum to 180°
  • ∠a and ∠c form a linear pair, so they sum to 180°
  • ∠a and ∠d are vertical angles, so they are congruent. m∠d = 120°
  • ∠a and ∠e are corresponding angles, so they are congruent. m∠e = 120°
  • ∠d and ∠f are same side interior angles, so they are congruent, which means they are supplements. So, 120° + m∠f = 180°; m∠f = 60°
  • ∠a and ∠g are same side exterior angles, so they are supplementary. So, 120° + m∠g = 180°; m∠g = 60°
  • ∠a and ∠h are alternate exterior angles, so they are congruent. So, m∠h = 120°

Problem Solving

The previous example showed just one option to find an angle measure through there are other possibilities to find each angle.

Again, the theorems are only true when the lines are parallel.

Now let's incorperate this information to solve algebra problems.

Example #3

Open Apply Properties of Parallel Lines Cut by a Transversal to Solve for Unknown Values in a new tab