Learn
Vocabulary
In this lesson we will construct and prove theorems about perpendicular lines.
Vocabulary
- Perpendicular Lines
- Perpendicular Bisector
Perpendicular Lines
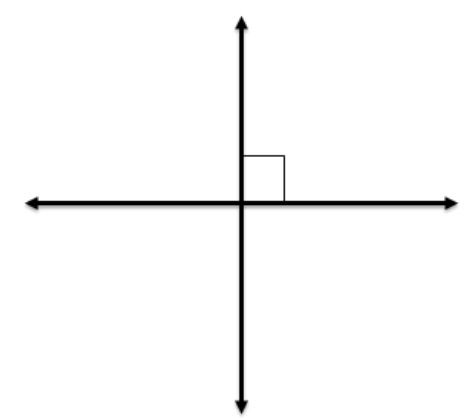
Another important pair of lines in geometry that we discussed in Unit 2 are perpendicular lines. Remember that perpendicular lines intersect to form a right angle.
A box will be located in the angle to identify that it is a right angle.
The next three theorems are based on the concept of perpendicular lines.
Theorem 1
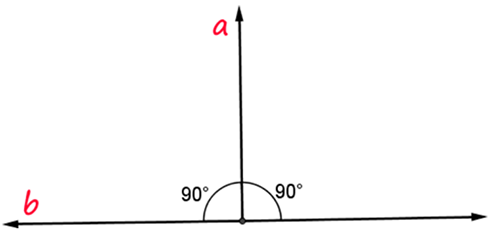
If two lines intersect to form a linear pair of congruent angles, then the lines are perpendicular.
Theorem 2
If two lines nonadjacent sides of two acute adjacent angles are perpendicular then the angles are complementary.
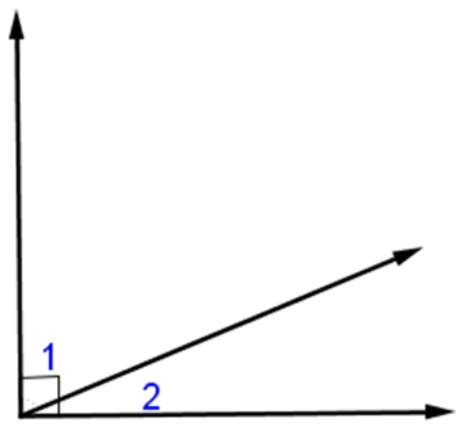
m∠1 + m∠2 = 90°
Theorem 3
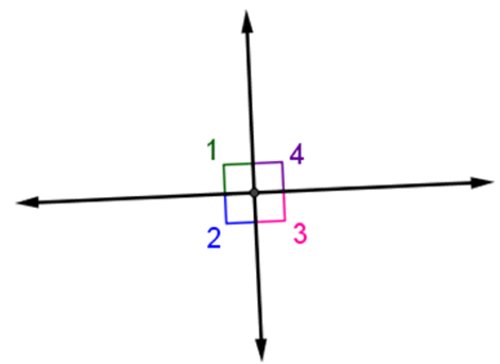
If two lines are perpendicular, then they intersect to form four right angles.
Exercise #1
Open Apply Properties of Perpendicular Lines to Find Unknown Values and Angle Measures in a new tab
Constructing Perpendicular Lines
The distance from a line to a point not on the line is the length of the segment perpendicular to the line from the point.

Example #2
The distance from the creek to the schoolhouse is the distance along a perpendicular path from the school to the creek.
Constructing Perpendicular Lines
Postulate: If given a line and a point not on the line, then there exists exactly one line through the point that is perpendicular to the given line.
Exercise #3
Open Construct Perpendicular Lines with a Compass and a Straight Edge in a new tab
Exercise #4
Open Construct a Perpendicular Bisector with a Compass and a Straight Edge in a new tab
Example #5
Open Construct a Perpendicular Bisector Using GeoGebra in a new tab