Try It
Equations of Parallel Lines Practice
Practice Problem #1
Give the slope of each line. Are the lines parallel?
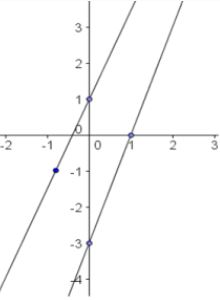
Slope of line a ___
Answer: 2
Slope of line b ___
Answer: 3
Are they parallel?
Answer: no
Practice Problem #2
Give the slope of each line. Are the lines parallel?

Slope of line a ___
Answer: -1
Slope of line b ___
Answer: -1
Are they parallel?
Answer: yes
Practice Problem #3
Are the lines parallel?
y = 3x + 4 and y = 3x - 2
Answer: yes; Since these equations are in slope intercept format, you can use the coefficient of the x-term as slope. Both of the coefficients here are three, so these lines are parallel.
Practice Problem #4
Are the lines parallel?
y - 3x = 5 and y = -3x + 2
Answer: no
Practice Problem #5
Find the equation of a line in slope intercept form that is parallel to the line ![]() and goes through the point (4, 1).
and goes through the point (4, 1).
Start by finding the slope of the line.
Since the lines are parallelm what is the slope?
Answer: 0.5
Ok, now that we know that the slope of the line will be 1/2 we can plug the slope and point into the point slope equation.
y - y = m(x - x1)

Distribute the coefficient outside the parentheses to simplify.
![]()
Answer: 1