Learn
Equations of Parallel Lines
Parallel lines are lines that never intersect. Below are examples of parallel lines.


Notation- Parallel Lines
To let you know that the lines are parallel they will be marked with symbols as shown below. Also, they can be stated they are parallel using the following notation:
![]()
Equations of Parallel Lines
Let us begin by proving that parallel lines have the same slope.
Given: the lines are parallel.
Prove: the slopes are equal using the slope formula.
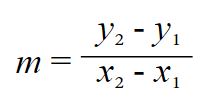
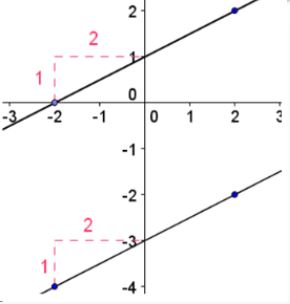
Since both lines have a slope of 1/2 then we conclude that parallel lines on a coordinate plane have the same slope.
Example #1
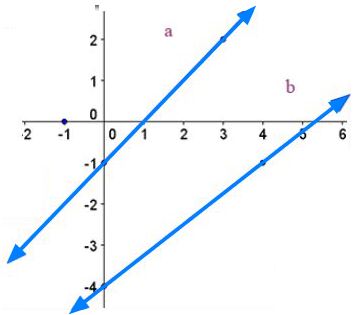
Give the slope of each line. Are the lines parallel?

Slope of line a ___
Answer: -2
Slope of line b ___
Answer: -2
Are they parallel?
Answer: yes
Example #2
Give the slope of each line. Are the lines parallel?
Slope of line a ___
Answer: 1
Slope of line b ___
Answer: 3/4
Are they parallel?
Answer: no
Finding Equations of Parallel Lines
Awesome! Now that you can identify parallel lines on a coordinate plane by identifying their slopes, we will go on to our next objective. We will now learn how to determine the equation of a line that is parallel to another line that goes through a given point.
Example #3
Summary
In summary follow these steps to answer the problem:
- Find the slope of the first line using slope formula.
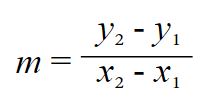
- Substitute the slope and the given point into the point slope equation. y - y1 = m(x - x1)
- Simplify the equation by putting it into slope intercept form. y = mx + b
Why can’t we use b?
You may be asking, "Can’t we just find the y-intercept from the graph?" That is true, you can answer this problem by graphing to find the y-intercept and then writing the equation in slope intercept form. Just remember that not all lines will go through a whole number on the y-axis and you will then have to solve the problem algebraically.