Learn
In this lesson we will learn about the slope of a line.
The slope of a line is like an incline or a hill. When the line is on the coordinate plane, the numbers tell us how steep it is.
The numbers that describe the slope are written in the form of a ratio or a fraction.
Slope Definition
As you probably remember, this ratio is described as 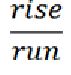
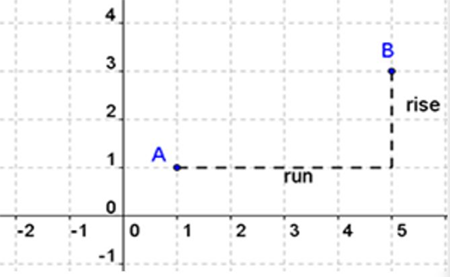
Rise describes how much we move up or down from one point to the next. Run describes how much we move left or right from one point to the next.
Go to Explore! Slope to find out more.
Slope Example
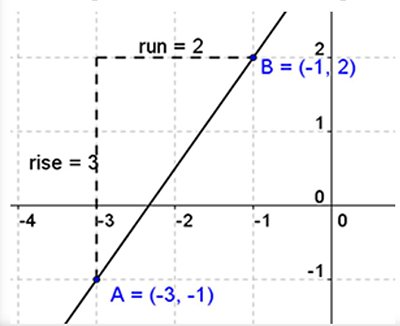
Notice in the graph below to get from point A to point B we moved up 3 and right 2.
So the slope of a line between these points is ![]()
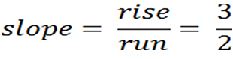
Slope Equation
We can also find the slope without to graph the point. This can be done using the slope formula. Notice that the variable (m) is used to represent slope.
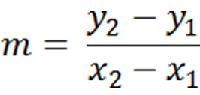
See if you can use the given points to find the value of slope.
Answer: 2 - -1 / -1 - -3
Answer: 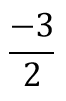
Slope of a Line
You can tell a lot about the slope by how it slants.
Positive Slope
Negative Slope
Undefined Slope
Zero Slope
Open Find the Slope between Two Points on a Coordinate Plane Using the Slope Formula in a new tab
Equation of a Line
Now that you remember how to find slope between two points, let's look at lines. Remember that between any two points there is only one line. Not only can we describe the steepness of the line using slope but we can also assign a unique equation. This is called a linear equation. The key word in "linear" is line.
There are two common forms of writing a linear equation. Select the parts of the equation to learn more.
Standard form: Ax + By = C
Slope-intercept form: y = mx + b
In this unit we will focus on slope intercept form. Slope intercept form allows us to quickly graph lines using the values that are in the m and b positions of the equation.
y = mx + b
m is the slope of the line
b is the y-intercept of the line. In other words, y-intercept is where the line intersects the y-axis.
Click on the y-intercept in this diagram.
Practice
Which graph matches this equation: y = -2x - 3.
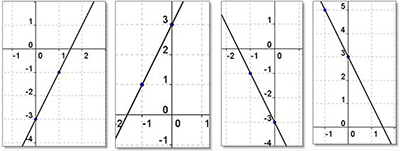
Answer: The third graph
Slope Intercept Form
See how much easier graphing lines can be when they are in slope intercept form? The only problem is that not all linear equations are in slope intercept form. The good news is that with a little algebraic maneuvering we can always put the equation in slope intercept form.
Changing to Slope Intercept Form
An example would be when the equation is in standard form such as 3x + 2y = 6. Our objective will be to get the y by itself on the left side of the equation. The following are the steps to make this happen. Select the lines for more information.
3x + 2y = 6
3x - 3x + 2y = 6 - 3x
2y = –3x + 6![[2y/2] = [(-3x+6)/2]](images/fraction3.png)
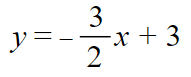
Open Rewrite a Linear Equation from Standard Form to Slope-Intercept Form in a new tab