Learn
Angle Pair Relationships
Angle relationships are very important in solving many geometry problems.
In your notebook, be sure to write the definitions as well as have drawings of examples of the terms listed.
Vocabulary:
- vertical angles
- linear pair
- complementary
- supplementary
Vertical Angles
Verticle angles are angles formed when two lines intersect. The vertical angles are those angles opposite each other having the same vertex, but no common side.
In this drawing m∠1 = m∠2 and m∠3 = m∠4.
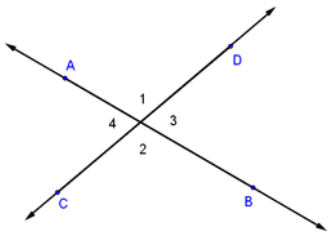
Reason:
When 2 lines intersect, the vertical angles are congruent.
For an interactive review visit Math Open Reference: Vertical Angles
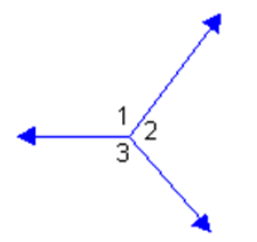
Important Note
Vertical angles are formed by two complete intersecting lines. In this diagram, there are no vertical angles because the angles are not formed by two complete intersecting lines.
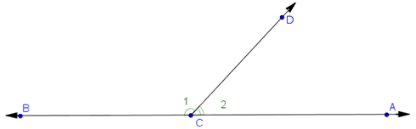
Linear Pair
In the drawing below we can say m∠1 + m∠2 = 180° because the measurement of a straight angle is 180°.
These two adjacent angles are called a linear pair because the two non-common sides form a straight line or opposite rays.
Go to Explore Linear Pairs to learn more
Review
Math Open Reference: Linear Pairs provides a wonderful interactive that illustrates linear pairs
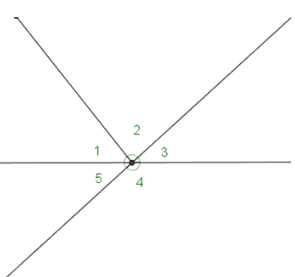
1. Are angles 1 and 2 a linear pair? Answer: no
2. Are angles 4 and 5 a linear pair? Answer: yes
3. Are angles 1 and 4 a linear pair? Answer: no
4. Are angles 3 and 5 a linear pair? Answer: no
Open Apply the Linear Pair Postulate and Vertical Angles Theorem to Find Unknown Values in a new tab
Open Apply the Linear Pair Postulate to Find Unknown Values in a new tab
Open Apply the Linear Pair Postulate and Vertical Angles Theorem to Find Unknown Values in a new tab
Complementary Angles
Complementary angles are two angles whose measures add up to 90°. They could either be adjacent or non-adjacent.
Each angle is the complement of the other angle.
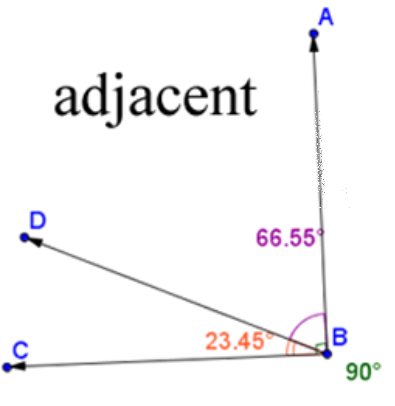
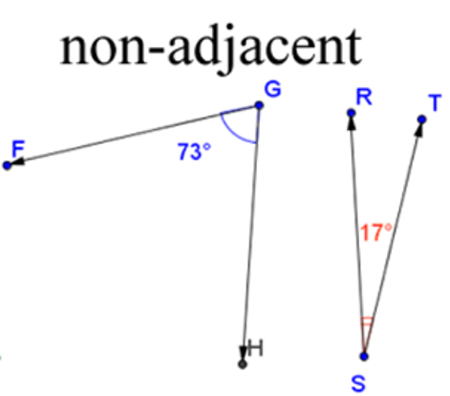
Open Apply Definitions of Complementary and Supplementary Angles to Find Angle Measures in a new tab