Learn

Adjacent and Congruent Angles

Remember to take good notes to study.

m∠ADB + m∠BDC = m∠ADC

 

An angle formed by rays D to A and D to C. Ray D to B comes out between the other two rays

Vocabulary

  • adjacent angles
  • measure
  • congruent angles
  • angle bisector
  • angle addition postulate

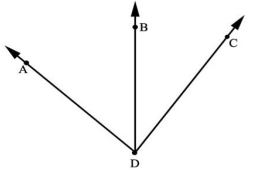
Adjacent Angles

Adjacent angles are two angles that share the same vertex and side. You cannot name angles such as these with just one letter because there is more than one angle at the vertex. In this case you would have to use three letters to name each angle. Remember, the vertex is always the middle letter.

One of these angles is ∠ ADB. What is the name of the other angle? ___

∠BDC or ∠CDB

Answer: ∠BDC

The Measure

Remember that it is very important to learn terminology and symbols to be successful in this course. Here are a few more new concepts.

When you see this written, m∠ AOC, it is read as “the measure of angle AOC.” In other words “measure” is abbreviated with the small caps letter m.

If a third ray divides an angle into two adjacent angles then we can say that the sum of the measures of the two adjacent angles is equal to the measure of the whole angle.

This is known as the Angle Addition Postulate.

m∠ADB + m∠BDC = m∠ADC

Open Apply the Angle Addition Postulate to Find Unknown Angle Measures in a new tab

Congruent Angles

Also, when two angles have the same exact measure they are called congruent angles.
The symbol for congruent is ≅ .

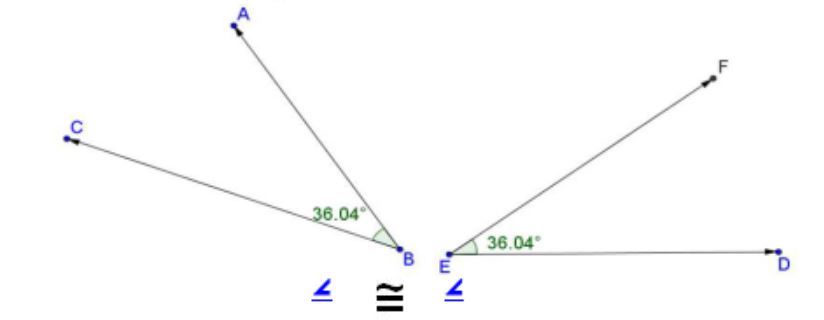
Two angles of equal measure 36.04 are shown, they are said to be congruent


We would write this as: ∠ ABC ≅ ∠ DEF

Congruent is basically a fancy word for equal. This symbol will be used often to identify that two or more figures are equal in size.

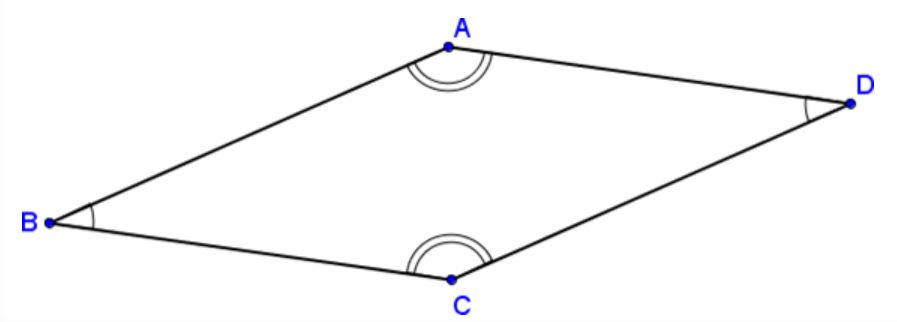
When drawing congruent angles, you use an arc in the middle of the angle to show that two angles are congruent. If two different pairs of angles are congruent, use one set of arcs for one pair, then two sets of arcs for the next pair and so on.

A parallelogram where A and C shown congruent with 2 dashes, with D and B shown congruent with 1 dash

Angle Bisector

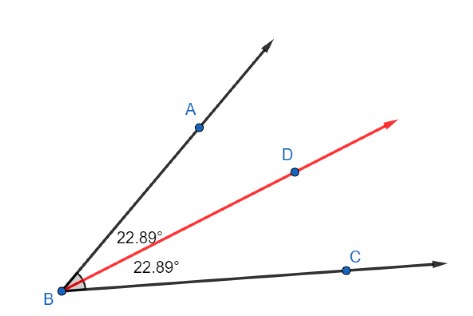
An angle bisector is a ray that divides an angle into two adjacent angles that are congruent.

In the diagram, angle BD bisects ∠ ABC because it divides the angle into two congruent angles, ∠ ABD and ∠ CBD. To identify congruent angles matching congruence arcs are placed inside the angles to show they are equal.

The angle A B C is split ray B to D into two equal angles

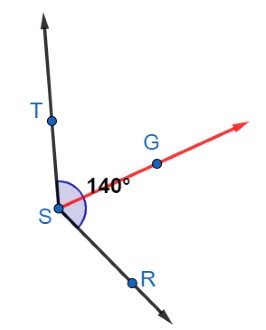
Angle Bisector Solution

An angle bisector divides an angle into two congruent angles, each of which has half the measure of the original angle. So,

 

m∠ RSG = m∠ GST = 1/2 (∠ RST)=1/2 (140°)=70°

The 140 degree angle T S R is split by ray S to G

Open Apply the Definition of an Angle Bisector to Find Unknown Values - Example #2 in a new tab

Open Apply the Definition of an Angle Bisector to Find Unknown Values - Example #3 in a new tab

Open Apply the Definition of an Angle Bisector to Find Unknown Values - Example #4 in a new tab