Learn

Segment Addition and Distance

Segment addition is really a simple concept. Basically, the length of a line segment is the sum of all of the smaller segments joined together to form it. Formally, this concept is called the segment addition or ruler postulate.

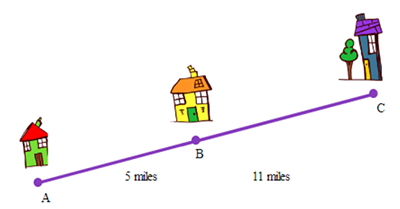
line with point A at one end, point B 5 miles from point A, point C at the other end which is 11 miles from point A; there are houses at each point

Segment Addition

If I ask you to determine how far it is from House A to House C, you can easily see that you need to add the distance from House A to House B to the distance from House B to House C.

So, the distance from House A to House C is: distance House A to House C = 5 miles + 11 miles distance House A to House C = 16 miles

Segment Notation

Of course we get tired of saying (not to mention writing) “the distance between House A and House C.” Instead we use symbols. When we name a line segment with endpoints A and C using symbols, we write AC. But if we want to denote the length of the line segment, or the distance between points A and C, we simply write AC with a line over the letters.

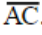
letters with line over

Suppose that I tell you that point B is between A and C. Note, that does NOT mean that B is exactly in the middle of points A and C, just somewhere between. Regardless of the position of B, as long as it is between A and C then we can refer to the distance between points A and C using symbols in this way: AC = AB + BC Remember, it doesn’t matter where point B lies along AC. As long as B is between A and C the above equation is correct.

line with point A on one end, point C on the other, and point B along with line closer to A than C

Segment Notation Example

Now, if we include actual lengths, measurements, on our picture, we can determine the measure of AC using our same equation.

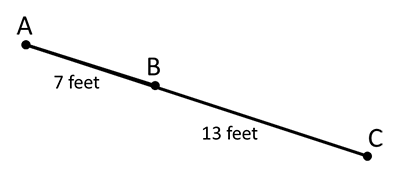
line with two segments: A to B is 7 feets; B to C is 13 feet

AC = AB + BC
AC = ? + ?
Add the length of the two segments together.
AC = 7 feet + 13 feet
So, AC = 20 feet

Postulate 1-1 The Ruler Postulate

The points on any line can be paired with real numbers so that given any two points P and Q on the line, P corresponds to zero, and Q corresponds to a positive 1.

line with two points: P which corresponds to 0 and Q which corresponds to 1

Postulate 1-2 Segment Addition Postulate

If R is between P and Q, then PR + RQ = PQ.

If PR + RQ = PQ, then R is between P and Q.

line with tthree points: P, Q, and R

Definition of Betweeness

Segments can be defined by using the idea of betweenness of points. In the figure, Point B is between A and C. For B to be between A and C, all three points must be collinear and B must lie on AC.

line segment with 3 points: A, B, and C

Line segment AB, consists of points A and B and all points between A and B. The measure of line segment AB, written AB, is the distance between A and B.  Thus, the measure of a line segment is the same as the distance between its two endpoints.

Distance

The measure of distance is always a positive value.  If you were asked how far you had walked you would not say -5 miles .... you would say 5 miles.  The direction in which you traveled made no difference to the actual distance.

Difference of the Coordinates

The distance between two points on a number line is the absolute value of the difference of the coordinates.

line with several points A is at -3.5; B is at -2; C is at 1; D is at 3

BC = | B - C |
Use the coordinate of B and C
BC = |-2 - 1|
BC = 3

The distance between two points on a number line can also be found by counting the distance between the two points. Remember the distance is always positive. It is three whole steps from B to C.

AB = 1.5
BA = 1.5
Count the spaces between A and B

CB = 3
BC = 3
Count the spaces between B and C

BD = 5
DB = 5
Count the spaces between B and D
It does not matter if you start with B or D to find the distance.

Distance Formula

Special Notation for Points on a Coordinate Plane

We use special notation to distinguish between two points on a coordinate plane. One point we will label (x1, y1) and the other point will be labeled (x2 , y2). It does not matter how you label either point. For our example I will label (1, 2) as (x1, y11) and (4, 3) as (x2 , y2). The rest is just placing the values into the correct location of the formula.

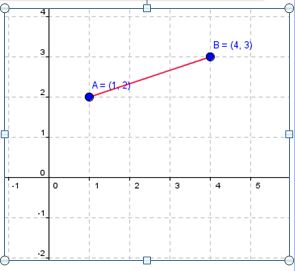
graph with point A at (1, 2) and point B at (4, 3) with a line segment going between the points.

Derive the Distance Formula

You can use the Pythagorean Theorem to derive the formula to find the distance between any two points A and B on a coordinate plane.

A right triangle in a coordinate plane. The hypotenuse of the triangle is segment AB. A is labeled (xsub1,ysub1) and B is labeled (xsub2,ysub2).

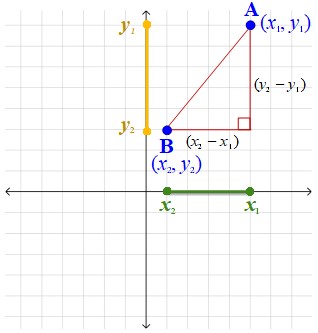
  1. To begin, label the coordinates of point A, (x1, y1) and the coordinates of point B, (x2, y2).
  2. Construct right angle using a vertical line segment that passes through point A and a horizontal line segment that passes through point B.
  3. Construct a line segment between points A and B. The figure formed is a right triangle. Segment AB is the hypotenuse and the other two sides are the legs.

    4. Now find the lengths of the legs of the right triangle.

  4. Subtract the x-values to find the length of the horizontal leg.
  5. Subtract the y-values to find the length of the vertical leg.
  6. Use the Pythagorean Theorem, c2 = a2 + b2, to find the distance between points A and B which is denoted by AB.
    1. Let a be the length of the horizontal leg which is x2 − x1.
    2. Let b be the length of the vertical leg which is y2 − y1.
    3. Let c is the length of segment AB which is denoted by AB.
    4. Substitute in x2 − x1 for a, y2 − y1 for b, and AB for c.

      5. AB2 =

      Take the square root of both sides.

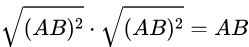
      Simplify the square root of open paren A B close paren squared times the square root of open paren A B close paren squared equals A B

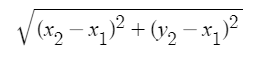
      = the square root of open paren x sub 2 minus x sub 1 close paren squared plus open paren y sub 2 minus x sub 1 close paren squared

Formula

The formula for finding the distance between two points on a coordinate plane is given below. We’ll talk more about where this formula comes from later.

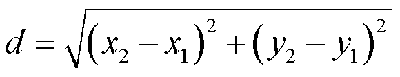
d = square root of [(x subscript 2 - x subscript 1) to the 2nd power + (y subscript 2 - y subscript 1) .

Distance Formula Example #1

Open Finding the Distance Between Two Points, A and B, on a Coordinate Plane in a new tab

Distance Formula Example #2

Open Apply the Distance Formula to Find the Distance Between Two Points Given Their Coordinates in a new tab

Distance Formula Example #3

Find the distance between A(5, –1) and B(3, 7).

Step 1: Label the coordinates of point A, (x1, y1) and the coordinates of point B, (x2, y2).

A(5,−1), B(3,7)

Step 2: Write the distance formula.

Step 3: Substitute in the values:

  • 3 for x2,
  • 5 for x1,
  • 7 for y2, and
  • −1 for y1.

Step 4: Use the order of operations to simply what's under the radical symbol.

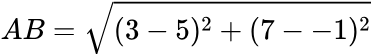
A B equals the square root of open paren 3 minus 5 divided into squared plus open paren the square root of 7 minus negative 1 close paren squared

Change the double signs "− −" to a plus sign.

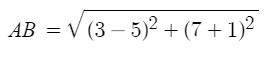
A B equals the square root of open paren 3 minus 5 close paren squared plus open paren 7 plus 1 close paren squared

Simplify the first set of parentheses. (3 − 5) = −2.

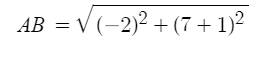
A B equals the square root of open paren negative 2 close paren squared plus open paren 7 plus 1 close paren squared

Simplify the second set of parentheses. (7 + 1) = 8.

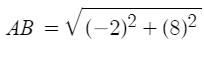
A B equals the square root of open paren negative 2 close paren squared plus 8 squared

Simplify the 1st exponent. (−2)2 = 4.

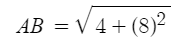
A B equals the square root of 4 plus 8 squared

Simplify the 2nd exponent. 82 = 64

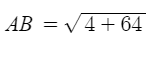
A B equals the square root of 4 plus 64

Add 4 + 64

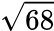
the square root of 68

Step 5: Write 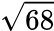the square root of 68 in simplified form.

To write in simplified form, you must rewrite 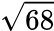the square root of 68 as a product of a perfect square and a number.

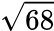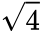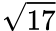The only way to rewrite the square root of 68 a product of a perfect square and a number is the square root of 4 × the square root of 17 .

AB = 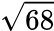the square root of 68

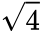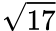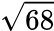
Substitute in the square root of 4 × the square root of 17 for the square root of 68

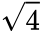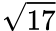
AB = the square root of 4 × the square root of 17

Take the square root of 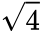the square root of 4

AB = 2 × 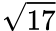the square root of 17

The distance between points A(5, −1) and B(3, 7) is:

AB =

Segment and Distance

Although football was used in the Introduction to discuss distance, a football field is not a good example of a number line. You could count by 10s on the number line but because 0 is not in the middle with negatives on the left and positives on the right, absolute value of the difference doesn't work.