Learn
Points, Lines, and Planes
Points, lines and planes are the most basic elements of geometry. To successfully solve geometry problems, it’s important to understand the purpose of these critical building blocks, how to read their diagrams, and how to name them properly. Points, lines and planes will be important throughout the course, so dig in and learn everything you can about them!
Geometry has its own language, so make sure you understand these very important vocabulary words before you move on to the next lesson.
- point
- line
- plane
- collinear
- coplanar
- intersection
- space
- line
- segment
- ray
Point
A point is the simplest geometric figure. It is represented by a dot on a page.
- A point indicates a location in space represented by a dot.
- A point has a location, but no size or shape. Points are named with a capital letter.
- On a graph the position of a point is named by an ordered pair: (x, y)
Practice Locating Points with GeoGebra. GeoGebra: Coordinate Points
Line
A line is a set of many points that extend without ending in opposite directions. A line can be named using any two points on the line, or with a single lowercase letter. The line shown here can be named line FE, line EF or line m. We place a line with arrows on both ends over the two capital letters to indicate that we are defining a line.
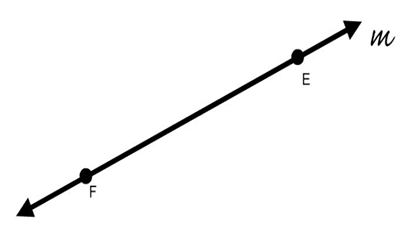
Lines and Points
We combine lines and points to describe geometric figures. Since all lines in geometry are straight, points on a line are called collinear. On the line shown here, points P, T, and B are collinear. Points P, T, and L are not collinear. In geometry, these are called non-collinear points.
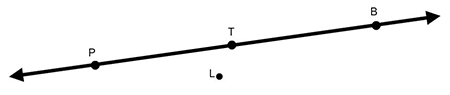
Line Segments
When you draw a line between any two points, you create a line segment. A line segment is part of a line.
We name a line segment with two endpoints. This line segment can be named segment AB or segment BA. Unlike a line, line segments have a beginning and an end, and therefore can be measured. We place a bar over the two capital letters to indicate that we are defining a line segment. So, we can name the line segment seen here as
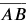
or
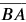
Ray
A ray extends endlessly in one direction. Unlike a regular line that extends endlessly in both directions, a ray has a defined starting point, like the light from a flashlight. A ray is named using the second letter on the side extending to infinity. The ray shown here would be named ray NP or NP with arrow over the letters NP.
Plane
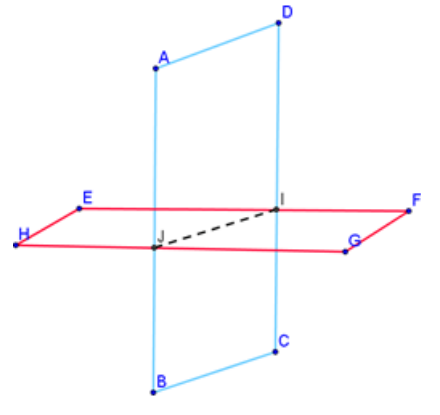
A plane is a flat surface that extends in all directions endlessly and has no thickness. It is a two dimensional surface with only length and width, but no height (or depth). To name a plane, you can use any three points on the plane, as long as they are not collinear. For example, we can name this plane ABC or planeCAB. We cannot name it plane CBD because these points are on a line and therefore are collinear. Points A, B, C, D are coplanar. Points C, B, D, I are noncoplanar.
Undefined Terms
The three undefined terms in geometry are: point, line, and plane. Although it is hard to explain these terms, we can give examples of each. Examples:
- Line: people standing in a straight line
- Point: a star in the sky
- Plane: a flat road sign
Intersection
Two lines intersect at a point.
Two planes intersect at a line.
Two lines intersect at a point.
Spaces
In geometry, a plane is a simple flat surface. On the other hand, space is a boundless, three-dimensional set of all points. Space contains points, lines, and planes. Practice Identifying Line Segments, Rays, and Lines with GeoGebra.
Parallel, Skew, and Perpendicular Lines
Definition of Parallel Lines
Parallel lines are lines that are on the same plane and never intersect.
Remember dark arrow symbols on the lines are used to identify that the lines are parallel to each other.
In the diagram below, line AB is parallel to line CD. You can use the parallel to symbol, ||, and the line symbol, ↔ , to write “line AB is
parallel to line CD” as 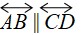 .
.
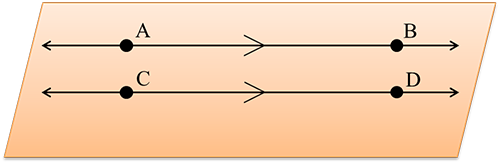
Parallel Lines
The definition of parallel lines states that they are on the same plane. This cube is an example of parallel lines when multiple planes are involved. Notice how OP and TS will never intersect even if the line segments were extended indefinitely. They are also located on the same plane. Since they are on the same plane and will never intersect w esay that OP and TS are parallel to each other.
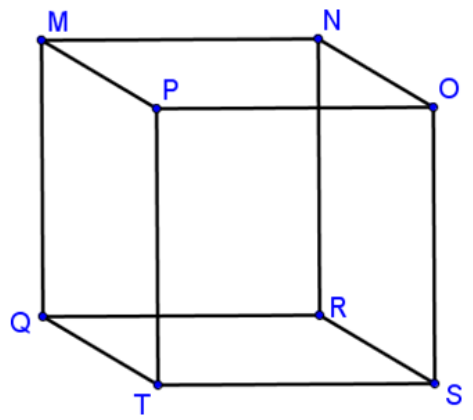
3D figure known as a cube is an example of a solid.
Skew Lines
There are other lines that do not intersect but ate not on the same plane. These are called skew lines. Notice in the diagram below that OP and QT will never intersect even if the line segments were extended indefinitely. Also, recognize that they are on different planes. Since they are not on the same plane and will never intersect we say that OP and QT are skew to each other.
Exercise #1
Look at the same cube above for this exercise.
MN and QR
Parallel
Skew
Answer: Parallel; MN and QR are in the same plane, so they are parallel.
Exercise #2
Look at the same cube above for this exercise.
PT and ON
Parallel
Skew
Answer: Skew
Perpendicular Lines
Another important pair of lines in geometry are perpendicular lines. Perpendicular lines intersect to form a right angle.
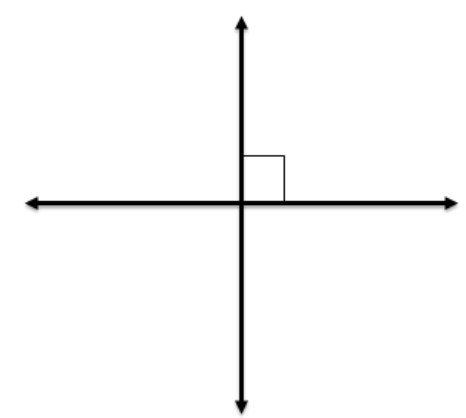
A box will be located in the angle to identify that it is a right angle.
Exercise #3
Let's see if you can identify which segments are perpendicular.

Are MN and ON perpendicular?
Answer: Yes
Exercise #4
Look at the same cube above for this exercise.
Are MP and QT perpendicular?
Answer: No
Planes
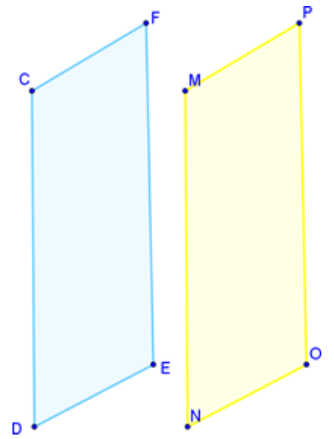
Planes can also be parallel or perpendicular. If you are sitting in a typical classroom right now, then you can look up at the ceiling and down at the floor to identify a set of parallel planes. Now, notice how the wall and floor are perpendicular to each other.

In the diagrams, see how a line is formed when two planes intersect. You see the crease formed where the floor and wall meet. The crease is a line segment in geometry.
Exercise #5
Planes are identified using three points on the plane. Now, identify parallel and perpendicular planes on the diagram.
Plane MNO and Plane NOR

Perpendicular
Parallel
Answer: Perpendicular; MNO and NOR meet at a right angle, so they are perpendicular.
Lines All Around Us
Parallel, perpendicular, and skew lines on planes are extremely important concepts because they are all around us. Below are few of the many examples of architecture that include each of these examples. How many of the concepts can you recognize?

