Learn
Pyramids
A pyramid is a polyhedron in which the base is a polygon and the lateral faces are triangles with a common vertex.
The height of a pyramid is the perpendicular distance between the base and the vertex. The slant height (l) is the altitude (height) of any lateral face.
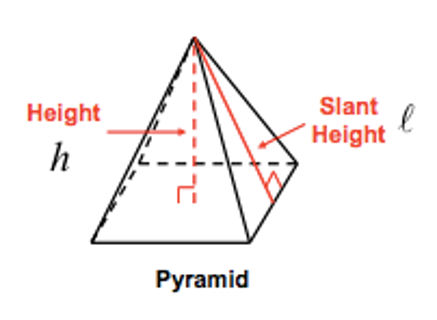
Surface Area of a Pyramid
The surface area, SA, of a regular pyramid is SA = B + ½Pl
Where B is the area of the base, P is the perimeter of the base and l is the slant height of the pyramid.
Example #1
Find the surface area of the regular pyramid shown.
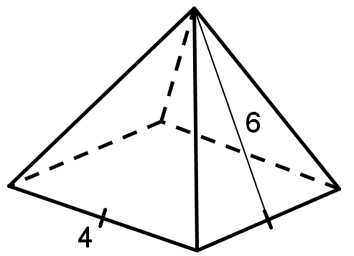
The equation for surface area is B + ½Pl. We don’t know B, so let’s solve for that first.
Start by finding the area of the base. The base is a square, so its area is s2.
- B = s2 Now, substitute the value of the side of the base into the equation.
- B = 42 Apply the exponent to solve. 42 = 4×4 = 16. Remember, area is in square units.
- B = 16 units
Now that we have the area of the base, let’s find the perimeter. We’ll need that for our surface area equation too. The perimeter of a square is found by the formula 4s, since all sides are congruent.
- P = 4s Substitute the value of the side length of the base into the formula
- P = 4(4) Simplify. 4(4) = 4×4 = 16
- P = 16 units
Now that we have B and P, we can substitute those values and the slant height into the formula to find the surface area.
- SA = B + ½Pl
- SA = 16 + ½ (16)(6)
- SA = 16 + 48
- SA = 64 units2
= 64 square units
Finding Slant Height
Sometimes you are given the height of the pyramid rather than the slant height. Use the Pythagorean Theorem to find the slant height, then find the surface area.
Example #2
Open Find the Surface Area of a Pyramid in a new tab
Cones
A cone has a circular base and a vertex that is not in the same plane as the base.
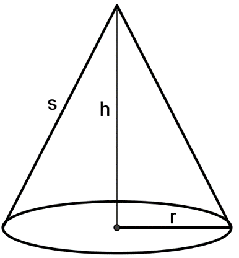
Height: the perpendicular distance between the vertex and the base
Right cone: cone whose height meets the base at its center
Slant height: the distance between the vertex and a point on the base edge
Lateral surface of a cone: consists of all segments that connect the vertex with points on the base edge
Surface Area of a Cone
The formula to find the surface area of a right cone is

where r is the radius of the base and l is the slant height.
Example #3
Find the surface area of the cone.
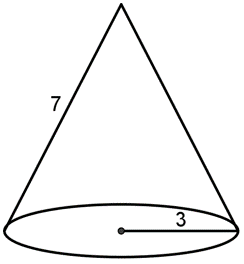
Start with the surface area formula for a cone.
- SA = πr2 + πrl Substitute the given values for the radius (3) and the slant height (7)
- SA = π(3)2 + π(3)(7) Simplify by applying the exponent and multiplying
- SA = 9π + 21π Simplify
- SA = 30 π units 2
Example #4
Open Find the Surface Area of a Cone in a new tab
Example #5
Open Find the Surface Area of a Regular Pyramid in a new tab