Learn
Pythagorean Theorem
Vocabulary
As you may recall the three angles in a triangle add to equal 180. Remember how if you had two angles you could find the third angle? Now we will learn more about the sides of a right triangle. Given two sides, we will now be able to find the third side of a right triangle.
Vocabulary
- Leg
- Hypotenuse
- Pythagorean
- Theorem
- Converse
- Pythagorean
- Theorem
Triangle
The three sides of a triangle have special names. The legs are the sides of the right triangle that form the right angle. The hypotenuse is the side opposite the right angle in a right triangle.
Pythagorean Theorem
The Pythagorean Theorem states that the hypotenuse squared equals the sum of the squares of the legs.
a2 + b2 = c2
Geometric View
This is a geometric view of the Pythagorean Theorem.
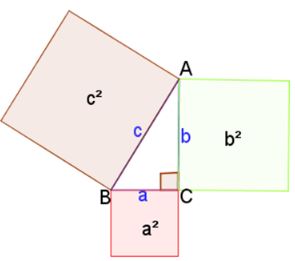
Note when each side is squares a square is drawn to indicate the side is squared.
a2 + b2 = c2
See if you can prove this yourself using GeoGebra:
- Pythagorean Theorem
- Pythagorean Theorem Visual
Example #1
Open Apply the Pythagorean Theorem to Find Segment Lengths of Right Triangles in a new tab
Example #2
Open Apply the Pythagorean Theorem to Find Segment Lengths of Right Triangles in a new tab
Example #3
Open Apply the Pythagorean Theorem to Find Segment Lengths of Right Triangles in a new tab
The Converse
The converse of the Pythagorean Theorem: If a2 + b2 = c2, then it is a right triangle. Let's look at a real world example where the carpenters have to be absolutely sure the walls are square!

Just plug in the sides to see if the statement is true.
152 + 202 = 252
The square all the terms.
225 + 400 = 625
Finally, add the numbers on the left side
625 = 625
Are both sides equal?
Yes! Since the sum of the squares of the sides equals the square of the hypotenuse, this triangle must be a right triangle. That's a good thing for the carpenter!