Learn
Writing Linear Equations
Graphing Review
Linear Equations
In prior lessons, you have learned many formulas.
In this lesson, we will represent the data (information as ordered paird) in a variety of ways: tables, graphs, equations in slope intercept form and standard form.
Key Concepts:
- ordered pairs
- tables
- graphs
- linear equations
- slope intercept form
- standard form
Table
In the last lesson you learned how to make an equation of a line in slope intercept form given two points on a line. The first objective for this lesson is very similar. You will be able to write the equation of a line in slope intercept form if you know more than two points on a line.
| x | y |
|---|---|
| -2 | 0 |
| 0 | 3 |
| 2 | 6 |
| 4 | 9 |
| 6 | 12 |
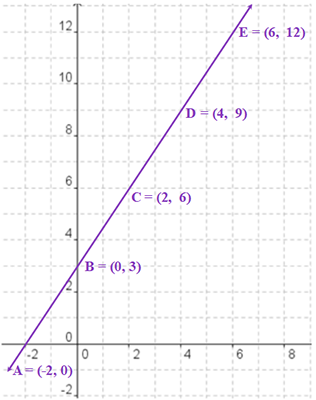
Slope Intercept Form
Writing Equations From a Table of Values
We are now going to learn how to write the equation of a line from a table of values. If you understood how to do it with two points from last lesson then you will love this - it's the same process!
Since the slope of a line never changes, we will do just like before, which is to either graph the line to find our slope and y-intercept or find them algebraically. Except this time, if we decide to do it algebraically, we get to choose our own two points to work with from a table of values. So if you did well last lesson you will do well again and if you had some trouble then you get to have another opportunity to have a better understanding.
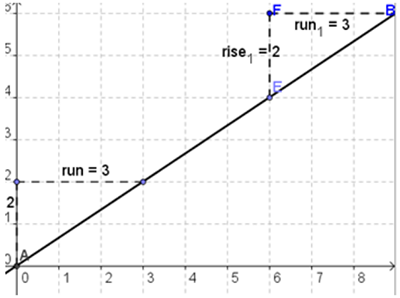
Example #1
Algebraic Approach
Finding the Equation Algebraically
See how much easier it is having an equation to solve future problems?
We obtained our equation from a graph but remember that we can also find it algebraically using the table of values.
| x | y |
|---|---|
| -2 | 0 |
| 0 | 3 |
| 2 | 6 |
| 4 | 9 |
| 6 | 12 |
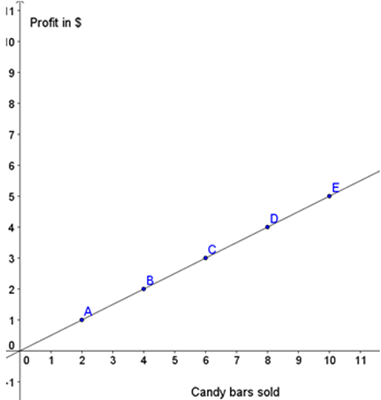
Example #2
Open Write the Equation of a Line in Slope-Intercept Form Using a Table of Values in a new tab
Standard Form
Slope Intercept Form vs. Standard Form
Slope intercept form is easy to write if you have the slope and the y-intercept:
y = mx + b
This form is also nice if you want to graph the line.
However, many linear equations are written in standard form, which is:
Ax + By = C
You can't just look at the letters A, B, and C and quickly graph this line. You have to rewrite into slope intercept form.
To rewrite the linear equation from standard form to slope intercept form, you isolate the y-term (place the y-term by itself on the left side of the equation and make sure it has a coefficient of 1):
Ax + By = C
y = mx + b
Example #3
Open Rewrite the Linear Equation from Standard Form to Slope-Intercept Form in a new tab