Learn

Slope

In this lesson we will learn about the slope of a line.

The slope of a line is like an incline or a hill. When the line is on the coordinate plane, the numbers tell us how steep it is.

The numbers that describe the slope are written in the form of a ratio or a fraction.

Slope Definition

As you probably remember, this ratio is described as 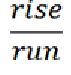rise over run

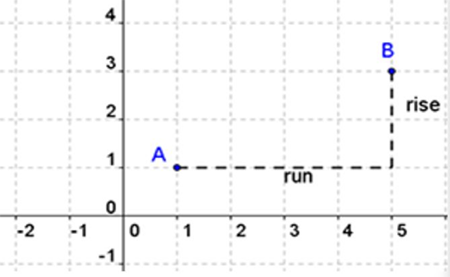
A graph showing that the rise is the vertical distance and run is the horizontal distance between two points (1,1) and (5,3) m equals the fraction with numerator y sub 2 minus y sub 1 and denominator x sub 2 minus x sub 1

Rise describes how much we move up or down from one point to the next. Run describes how much we move left or right from one point to the next.

Go to Explore! Slope to find out more.

Slope Example

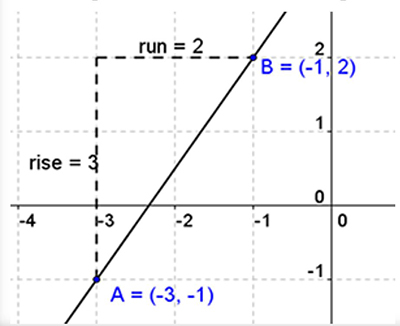
Notice in the graph below to get from point A to point B we moved up 3 and right 2.

So the slope of a line between these points is 3 over 2

Graph with point A at (-3, -1) and point B at (-1, 2). It shows the vertical distance 3 and a horizontal distance of 2

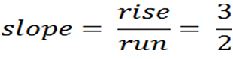
slope equals rise over run which equals 3 over 2

Slope Equation

We can also find the slope without to graph the point. This can be done using the slope formula. Notice that the variable (m) is used to represent slope.

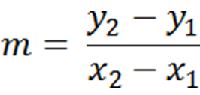
m equals change in y over change in x, which is (y2 - y1) over (x2 - x1)

 

See if you can use the given points to find the value of slope.

the slope formula, but with x and y values for each point missing.

Answer: 2 - -1 / -1 - -3

m equals blank over blank

Answer: -3/2

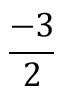
Slope of a Line

You can tell a lot about the slope by how it slants.

Positive Slope

A line that goes upward as it moves from left to right

Negative Slope

A line that goes downward as it moves from left to right

Undefined Slope

A vertical line

Zero Slope

A horizontal line

Open Find the Slope between Two Points on a Coordinate Plane Using the Slope Formula in a new tab

Equation of a Line

Now that you remember how to find slope between two points, let's look at lines. Remember that between any two points there is only one line. Not only can we describe the steepness of the line using slope but we can also assign a unique equation. This is called a linear equation. The key word in "linear" is line.

There are two common forms of writing a linear equation. Select the parts of the equation to learn more.

Standard form: Ax + By = C

Slope-intercept form: y = mx + b

In this unit we will focus on slope intercept form. Slope intercept form allows us to quickly graph lines using the values that are in the m and b positions of the equation.

y = mx + b

m is the slope of the line

b is the y-intercept of the line. In other words, y-intercept is where the line intersects the y-axis.

Click on the y-intercept in this diagram.

A line with point C at (0.44, 4.98) and D at ( negative 1.51, 0.4)

 

Practice

Which graph matches this equation: y = -2x - 3.

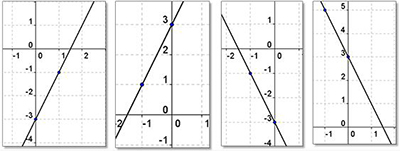
4 coordinate planes; the first plane shows a line passing through points (0, negative 3) and (1, negative 1); the second plane shows a line passing through points (negative 1,1) and (0,3), the 3rd plane shows a line passing through points (0, negative 3) and (negative 1, negative 1); the 4th plane shows a line passing through point (0, 3)

 

Answer: The third graph

Slope Intercept Form

See how much easier graphing lines can be when they are in slope intercept form? The only problem is that not all linear equations are in slope intercept form. The good news is that with a little algebraic maneuvering we can always put the equation in slope intercept form.

Changing to Slope Intercept Form

An example would be when the equation is in standard form such as 3x + 2y = 6. Our objective will be to get the y by itself on the left side of the equation. The following are the steps to make this happen. Select the lines for more information.

3x + 2y = 6
3x - 3x + 2y = 6 - 3x
2y = –3x + 6
[2y/2] = [(-3x+6)/2]
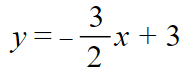
y= -(3/2)m>x</em> +3

Open Rewrite a Linear Equation from Standard Form to Slope-Intercept Form in a new tab