Guided Practice
Practice Problem #1
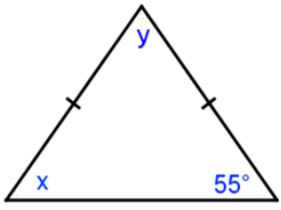
Solve for x and y.
Ok, let's start with identifying the given information. What information do we have here?
In this triangle, there are two ___ sides.
Answer: congruent
Correct, we have two congruent sides on this triangle. x and 55° are the two angles opposite these congruent sides. By the base angle theorem, x and 55° are ___.
Answer: congruent
That's right, x and 55° are congruent. So, x = ___
Answer: 55°
Great! Now that we know x = 55°, we can solve for y using the triangle sum theorem. By the triangle sum theorem, we know that the interior angles of a triangle sum to ____°.
Answer: 180°
Ok, now write an equation.
x + y + 55° = ___°
Answer: 180°
On to the next step: substitute in the known value for x.
___ + y + 55° = 180°
Answer: 55°
Great! Now, combine like terms on the left side of the equation.
y + ___° = 180°
Answer: 110°
Last step! Now, just isolate y to find its value.
y = ___°
Answer: 70°
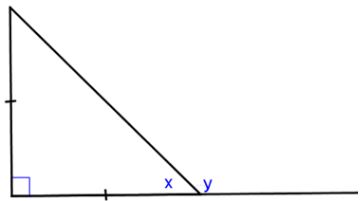
Practice Problem #2
Solve for x and y.
Ok, let's start by finding x. We only know one angle's value, the right angle. However, since x and the unlabeled angle are opposite two congruent sides, how is it related to the unlabeled angle? It is ___.
Answer: congruent
Yes, x and the unlabeled angle are congruent. So, the measure of that angle is ___.
Answer: x
Great. Now we know the measures of all angles in the triangle: 90, x, and x. Can we set up an equation to solve for x now?
90 + ___ + ___ = ___
Answer: x, x, 180
Good job! Now, simplify the left side of the equation.
90 + ___ = 180
Answer: 2x
Getting closer...Now we need to isolate the x term.
2x = ___
Answer: 90
Last step!
x = ___°
Answer: 45
Ok, so now we can x = 45. We can solve for y now. What is the relationship between x and y.
- They are vertical angles
- They form a linear pair
Answer: They form a linear pair
Correct, x and y are a linear pair. How are linear pair angles related?
- They are congruent
- They are complementary
- They are supplementary
Answer: They are supplementary
Ok, since x and y are supplements, we can now write an equation.
x + y = ___°
Answer: 180°
Great! Now substitute in the value of x, the one we just solved for.
___ + y = 180°
Answer: 180°
Last step! Just isolate y.
y = ___°
Answer: 135°