Isosceles and Equilateral Triangles

Remember that in the previous lesson we learned how to classify triangles. We will look closer at these two triangles:

  • Isosceles Triangles
  • Equilateral Triangles

Vocabulary:

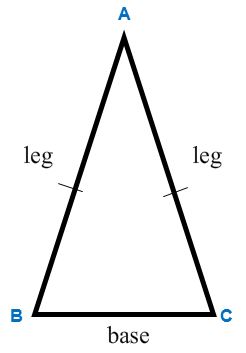
  • Leg
  • Base
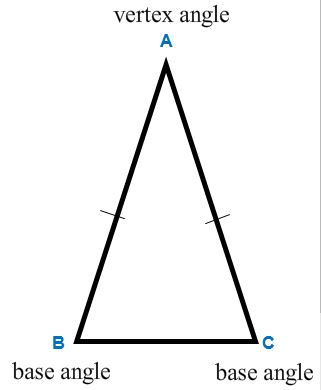
  • Vertex Angle
  • Base Angle
  • Base Angle Theorem
  • Isosceles Triangle
  • Equilateral Triangle
  • Equiangular Triangle
  • Corollary
  • Transformations
  • Reflection
  • Rotation

Isosceles Triangles

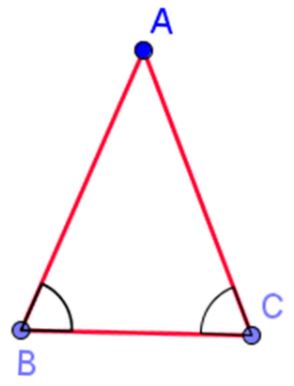
First we will focus on the properties associated with isosceles triangles. Below are characteristics of an isosceles triangle. The congruent sides are called the legs and the other side is the base.

A triangle where the 2 sides are equal and the third is not. The equal sides are called the legs and the other side is called the base

∠A is the vertex angle

∠B and ∠C are called the base angles

A triangle where 2 angles are equal and the third is not. The equal angles are called base angles and the third angle is the vertex angle

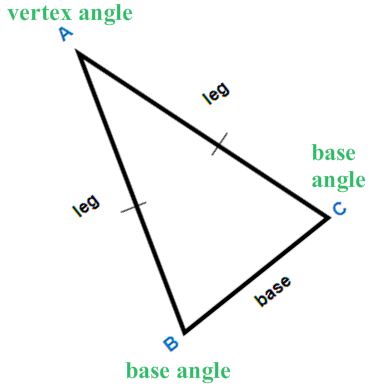
Please note that an isosceles triangle does not have to be sitting on its base. It can be rotated. It would not change the parts of the triangle.

In the isosceles triangle, the vertex angle is always where the legs intersect. The base is always between the base angles

Base Angles Theorem

Here is a theorem associated with isosceles triangles. Base angles theorem states that if two sides of a triangle are congruent, then the angles opposite them (called base angles) are congruent. If ∠AB ≅ ∠AC, then ∠B ≅ ∠C To find out more, go to Geogebra - Base Angles.

An isosceles triangle with a vertex angle called A and base angles calle B and C. Leg A B and leg A C are marked congruent

Converse to Base Angles

The converse is also true.

Converse to Base Angles theorem states that if a triangle has two congruent angles, then the sides opposite them are congruent.

If ∠B ≅ ∠C, then ∠AB ≅ ∠AC

Transformation

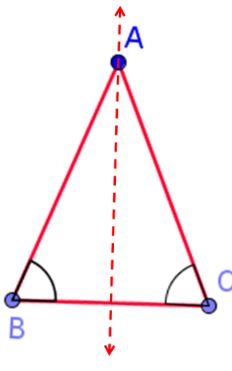
Recall that a line of symmetry is a line that when a figure is folded about the line the figure will land on itself. Could you draw a line of symmetry for the isosceles triangle to the right?

An isosceles triangle with a vertex angle called A and base angles calle B and C. The base angles are marked equal

When the line of symmetry is drawn, notice how angles B and C would land on each other when the triangle is folded about the line of symmetry.

Thus an isoscles triangle has a reflection that will carry onto itself.

An isosceles triagle with a vertex angle called A and base angles calle B and C. The base angles are marked equal and a line of symmetry is drawn from the base up to angle A

Recall that a rotation is when you turn the figure.

Could you rotate the isosceles triangle so that the rotation carries onto itself?

Yes or No?

Answer: No

Example #1

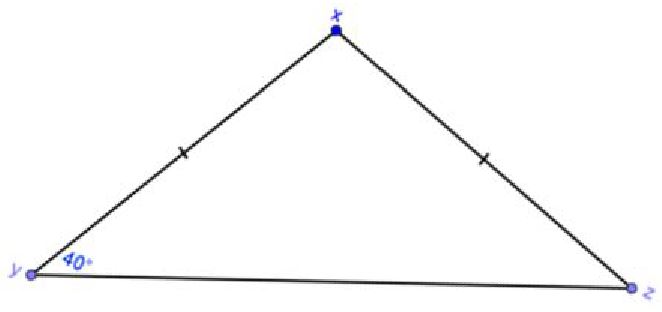
Find the missing angle measures x and z in the following triangle.

An isosceles triangles has equal legs. One of the base angles is 40 degrees

Solution: Since two sides are congruent we know the triangle is isosceles. Using the base angles theorem if two sides of a triangle are congruent, then the angles opposite them (called base angles) are congruent. we know that angles y and z are congruent, so angle z = 40°. The sume of all angles in a triangle is 180°, therefore we can use the following equation to solve for angle x.

x + y + z = ___°

Answer: 180°

x + ___ + ___ = 180°

Answer: x + 40 + 40 = 180°

x + ___ = 180°

Answer: x + 80 = 180°

x = ___°

Answer: x = 100°

Your Turn

You try one using the converse base angles theorem. Find the missing side length CD.

Let's start by reviewing the converse to the base angles theorem. if a triangle has two congruent angles, then the sides opposite them are congruent. What does it state? If a triangle has two congruent angles, then the sides opposite them are _________?

Answer: congruent

You try one using the converse to the base angles theorem. Find the missing side length CD.

Now you know that DE and CD are congruent. Using that information, what is the length of CD? ___

Answer: 7

Corollary

A result based on the base angles theorem called a corollary states that if a triangle is equilateral all sides have equal length , then it is equiangular all angles equal measure 60° .

The converse to that corollary states that if a triangle is equiangular, then the triangle is equilateral.

In other words, if a triangle has three congruent angles, it has three congruent sides. If it has three congruent sides, then it has three congruent angles.

A triangle where all the angles marked equal and all of the sides are marked congruent

Example #2

Find the missing angle measures.

Solution: Since all sides are congruent we know the triangle is equilatteral. The corollary states that an equilateral triangle is also equiangular. Since each angle is the same we can use x as the variable for each. Our equation will be as follows:

x + x + x = ___°

Answer: 180°

___ = 180°

Answer: 3x

x = ___°

Answer: 60°

Hence, each angle is 60°, no matter what the length of a leg is.

Translations?

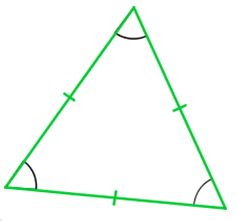
Recall that a line of symmetry is a line that when folded about the line the figure will land on itself.

A equilateral triangle with lines of symmetry shown. The lines of symmetry all follow exactly where altitudes exist

Could you draw a line of symmetry for the equilateral triangle to the right?

  • Yes
  • No

Answer: Yes

Is there more than one line of symmetry?

  • Yes
  • No

Answer: Yes

How many lines of symmetry?

  • 1
  • 2
  • 3

Answer: 3

Could you rotate the triangle onto itself?

  • Yes
  • No

Answer: Yes

Previous Page