Exterior Angles

Exterior Angle Theorem

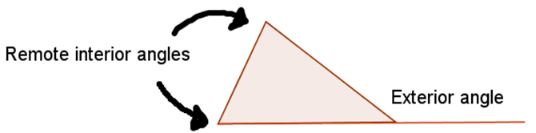
Let's look at another theorem in Geometry that is very helpful in solving problems. When a side of a triangle is extended an exterior angle is formed as shown below.

A triangle where a line extends out of the base to one side. Where the line extends out, it forms an obtuse angle with one side of the triangle labeled the exterior angle. The angles of the triangle opposite from where the line extends are labeled remote interior angles

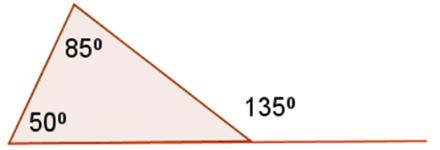
The Exterior Angle Theorem states that the exterior angle is equal to sum of the two remote interior angles.

A triangle where the exterior angle is 135 degrees and the interior angles are 50 degrees and 85 degrees

50° + 85° = 135°

Check out this Geogebra exercise for more information.

Remember, a proof is logical arguement for a statement. Recall the two column proof.

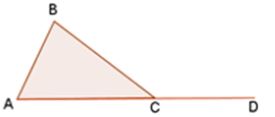
A triangle with an exterior angle. The remote interior angles are angle A and angle B. The third angle of the triangle is A C B and the exterior angle is B C D

Given: ∠ABC

Proof: m∠A + m∠B = m∠BCD

Statements:

  1. ∠ABC
  2. m∠A + m∠B + m∠ACB = 180°

Reasons:

  1. Given
  2. Triangle Sum Theorem
  3. Linear Pair

Look at this Proof!

Remember, a proof is logical arguement for a statement. Recall the two column proof.

A triangle with an exterior angle. The remote interior angles are angle A and angle B. The third angle of the triangle is A C B and the exterior angle is B C D

Given: ∠ABC

Proof: m∠A + m∠B = m∠BCD

Statements:

  1. ∠ABC
  2. m∠A + m∠B + m∠ACB = 180°
  3. m∠ACB + m∠BCD = 180°
  4. m∠A + m∠B + m∠ACB = m∠ACB + m∠BCD
  5. m∠A + m∠B + m∠BCD

Reasons:

  1. Given
  2. Triangle Sum Theorem
  3. Linear Pair
  4. Substitution
  5. Subtraction

Watch this video for more information.

Your Turn

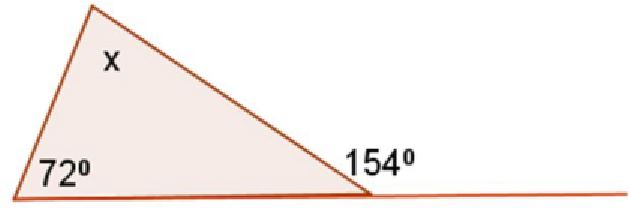
Find the value of x. Which theorem should you use?

  • The interior angles of a triangle sum to 180°
  • The exterior angles of a triangle sum of the two remote interior angles.

A triangle where the remote interior angles are angle 72 degrees and X degrees. The exterior angle is 154 degrees

Answer: The exterior angles of a triangle sum of the two remote interior angles.

Which formula should you use?

  • x + 72° + 154° = 180°
  • x + 72° = 180°
  • x + 72° = 154°

Now it is one step to solve.

x + 72 = 154

x = ___

Answer: 82

Previous Page