Guided Practice
Practice Problem #1
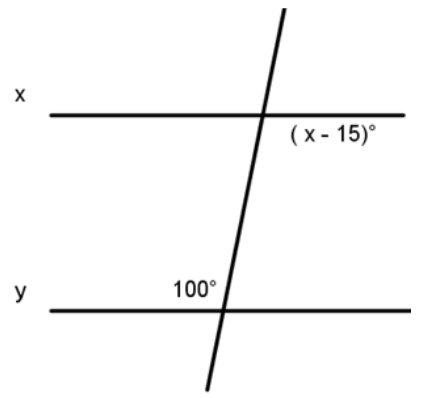
What must x equal for these lines to be parallel?
Let's start by identifying the relationship between these angles.
- alternate interior
- corresponding
- same side interior
- vertical
- alternate exterior
- linear pair
- same side exterior
Answer: alternate interior
Ok, we know these are alternate interior angles. What is the relationship between these angles?
- congruent
- complementary
- supplementary
Answer: congruent
Correct! Alternate interior angles are congruent. Which equation should we use to solve for x?
- x - 15 + 100 = 90
- x - 15 = 100
- x - 15 + 100 = 180
Answer: x - 15 = 100
Correct! Now we just solve.
x - 15 = 100
x = ___
Answer: 115
Practice Problem #2
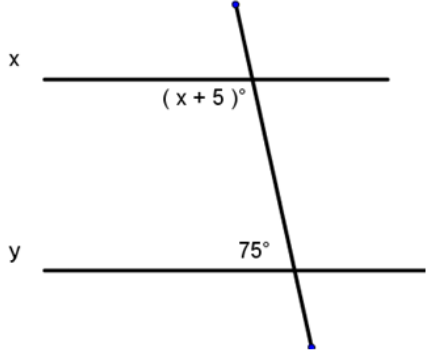
What must x equal for these lines to be parallel?
Let's start by identifying the relationship between these angles.
- alternate interior
- corresponding
- same side interior
- vertical
- alternate exterior
- linear pair
- same side exterior
Answer: same side interior
Ok, we know these are same side interior angles. What is the relationship between these angles?
- congruent
- complementary
- supplementary
Answer: supplementary
Correct! Same side interior angles are congruent. Which equation should we use to solve for x?
- x + 5 + 75 = 90
- x + 5 = 75
- x + 5 + 75 = 180
Answer: x + 5 + 75 = 180
Great! Now, just solve.
x + 5 + 75 = 180
x + ___ = 180
Answer: 80
x = ___
Answer: 100
Practice Problem #3
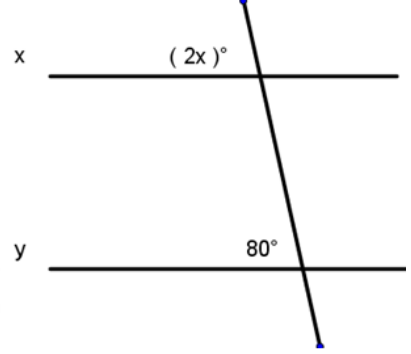
What must x equal for these lines to be parallel?
Let's start by identifying the relationship between these angles.
- alternate interior
- corresponding
- same side interior
- vertical
- alternate exterior
- linear pair
- same side exterior
Answer: corresponding
Ok, we know these are corresponding angles. What is the relationship between these angles?
- congruent
- complementary
- supplementary
Answer: congruent
Correct! Corresponding angles are congruent. Which equation should we use to solve for x?
- 2x + 80 = 90
- 2x = 80
- 2x + 80 = 180
Answer: x + 5 + 75 = 180
Now, just solve.
2x = 80
x = ___
Answer: 40