3.03 Parallel Lines and Transversals

Problem Solving

Angle Measures

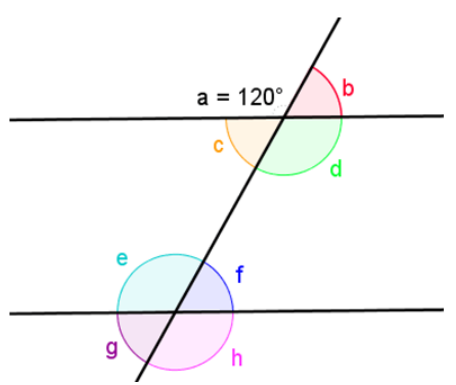
Awesome! Now that you can identify each pair of angles, let's apply this information to solve problems. If we know just one angle measure then we can find the other seven angle measures when the two parallel lines are intersected by a transversal. Select each angle to see its measure and how it related to the given angle measure.

Relative to angle a, angle b is a linear pair, angle c is a linear pair, angle d is a vertical angle, angle e is a corresponding angle, angle g is same side exterior angles, angle h is an alternate exterior angle, and angle f has no named relation but is a corresponding angle to the vertical angle of a

Problem Solving

The previous example showed just one option to find an angle measure through there are other possibilities to find each angle.

Again, the theorems are only true when the lines are parallel.

Now let's incorperate this information to solve algebra problems.

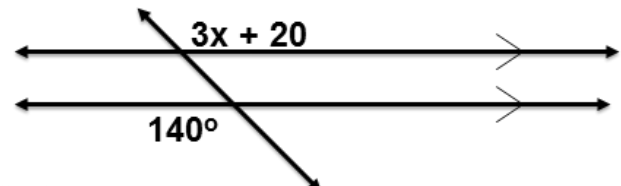
Example #1

Find x

2 parallel horizontal lines are cut by a transversal. The obtuse exterior angle on the top has value 3x+20 and the obtuse exterior angle on the bottom has value 140

Solution: First identify the angle pair relationship. In this problem, (3x + 20) and 140 are alternate exterior angles. We learned from the theorem that the alternate exterior angles are congruent when two parallel lines are cut by a transversal.

Since these angles are congruent, we will set up the equation as follows:

3x + 20 = 140

3x = 120

x = ___

Answer: 40

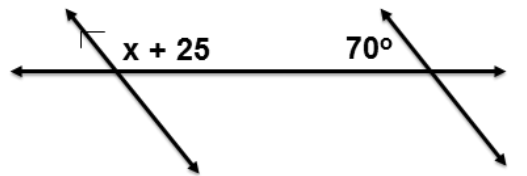
Example #2

Find x

2 parallel vertical lines are cut by a transversal. The interior angle on the upper left has value x+25 and the interior angle on the upper right has value 70

Solution: Again, we need to identify the angles. The angles (x + 25) and 70 are same side interior angles. We know that same side interior angles are supplementary when two parallel lines are cut by a transversal.

Since these angles are supplementary, our equation this time will be:

(x + 25) + 70 = ___

Answer: 180

x + ___ = 180

Answer: 95

x = ___

Answer: 85