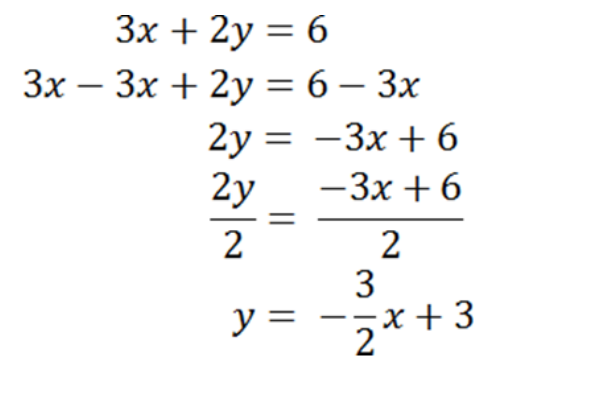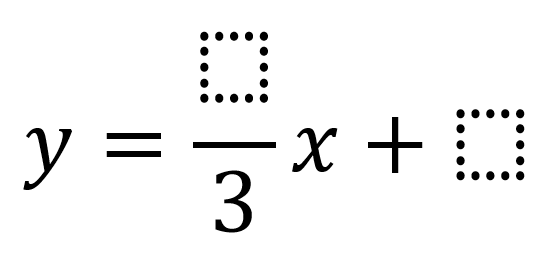Linear Equations
Equation of a Line
Now that you remember how to find slope between two points, let's look at lines. Remember that between any two points there is only one line. Not only can we describe the steepness of the line using slope but we can also assign a unique equation. This is called a linear equation. The key word in "linear" is line.
There are two common forms of writing a linear equation. Select the parts of the equation to learn more.
Standard form: Ax + By = C
Slope-intercept form: y = mx + b
In this unit we will focus on slope intercept form. Slope intercept form allows us to quickly graph lines using the values that are in the m and b positions of the equation.
y = mx + b
m is the slope of the line
b is the y-intercept of the line. In other words, y-intercept is where the line intersects the y-axis.
Click on the y-intercept in this diagram.
Linear Equation Video
Visit this interactive site to review using the linear equation in slope intercept form to graph a line: PH School Slope Video.
Practice
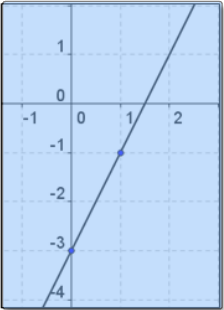
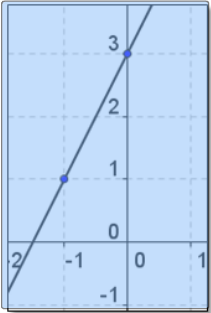
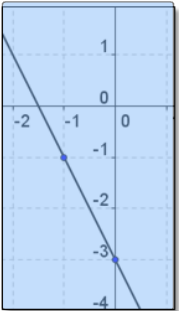
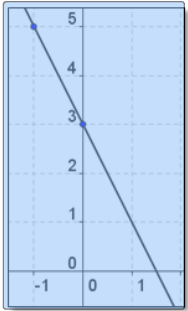
Match the correct graph from the equation. Click to select the graph y = -2x - 3.
A.
B.
C.
D.
Answer: C.
Slope Intercept Form
See how much easier graphing lines can be when they are in slope intercept form? The only problem is that not all linear equations are in slope intercept form. The good news is that with a little algebraic maneuvering we can always put the equation in slope intercept form.
Changing to Slope Intercept Form
An example would be when the equation is in standard form such as 3x + 2y = 6. Our objective will be to get the y by itself on the left side of the equation. The following are the steps to make this happen. Select the lines for more information.
Practice
Place -4x + 3y = 12 in slope intercept form.
Start by isolating the y term. What can you do to eliminate the x term from the left side of the equation?
___ - 4x + 3y = 12 + ___
Answer: 4x, 4x
Simplify
___ = 4x + 12
Answer: 3y
What can you divide both sides by to isolate y?
Answer: 3
Simplify your answer.
Answer: 4, 4