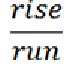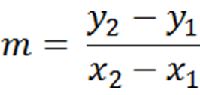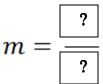Slope
In this lesson we will learn about the slope of a line.
The slope of a line is like an incline or a hill. When the line is on the coordinate plane, the numbers tell us how steep it is.
The numbers that describe the slope are written in the form of a ratio or a fraction.
Slope Definition
As you probably remember, this ratio is described as
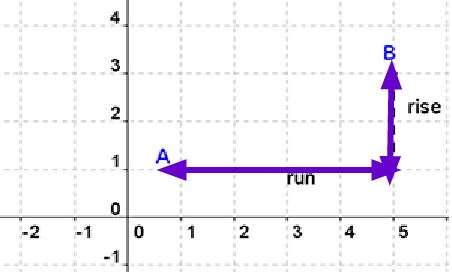
Rise describes how much we move up or down from one point to the next. Run describes how much we move left or right from one point to the next.
Go to Explore! Slope to find out more.
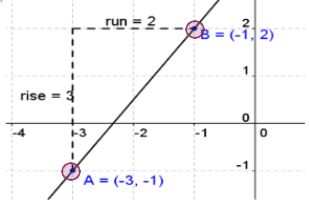
Slope Example
Notice in the graph below to get from point A to point B we moved up 3 and right 2.
So the slope of a line between these points is
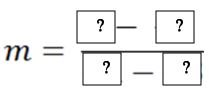
Slope Equation
We can also find the slope without to graph the point. This can be done using the slope formula. Notice that the variable (m) is used to represent slope.
Slope Equation Example
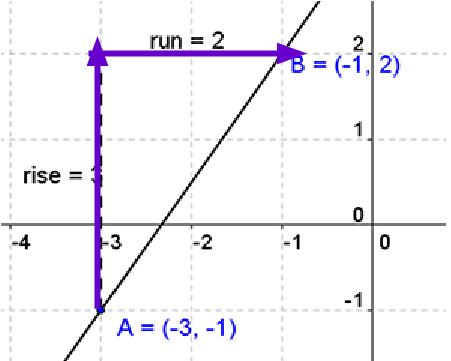
Remember from Unit 1 that when working with two points we use special notation to seperate the points. One point we will label (x1, y1) and the other point will be labeled (x2, y2). It does not matter how you label either point. For our example we will label A(-3, -1) as (x1, y1) and B(-1, 2) as (x2, y2). The rest is just placing the values into the correct location of the formula.
See if you can use the given points to find the value of slope.
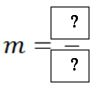
Answer: 2 - -1 / -1 - -3
Answer: -3/2
Slope Video
For a quick interactive view on how to find slope as well as learn information that will help you answer questions on the task assignment visit this site: PH School Slope Video
Slope Practice
Alright, now it is your turn to find slope.
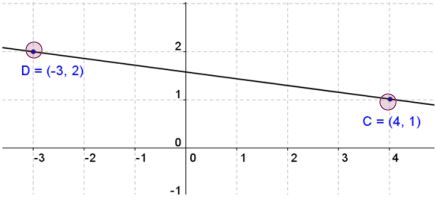
Find the slope of a line that goes through the points C(4, 1) and D(-3, 2). Let C be (x1, y1) and D be (x2, y2).
See if you can use the given points to find the value of slope. Substitute in the appropriate values.
Answer: 2 - 1 / -3 - 4
Answer: 1/-7
Slope of a Line
You can tell a lot about the slope by how it slants.
Positive Slope
Negative Slope
Undefined Slope
Zero Slope