Segment Partitions

For your notebook, be sure to include the vocabulary for this section and the Midpoint Formula

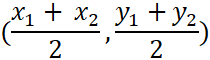
The midpoint formula. The average of the x values gives your new x value and the average of your y values gives your new y value: (half the sum of x1 and x2, half the sum of y1 and y2)

given points (x1 , y1) and (x2 , y2).

Vocabulary

  • congruent
  • ration
  • midpoint
  • supplementary
  • segment
  • bisector

From the previous lesson we know a line segment can be divided into smaller line segments.

The whole is simply the sum of its parts.

AB + BC = AC

6 in + 3 in = 9 in

A point can partition the segment in a given ratio. A ratio is a fraction that describes the relationship between two numbers such as the segment partitions.

Example: The ratio between AB and BC is AB over BC = 6 over 3 = 2 over 1 = 2 or 2

State the ratio of the two line segment partitions.

The line segment A to C is broken into A to B of length 2 and B to C of length 10

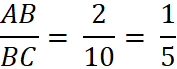
AB over BC = 2 over 10 = 1 over 5

Check It!

Sometimes a point partitions a segment with a ratio .

When this happens partitions have equal length measurement which means the segments are congruent.

The symbol for congruent is ≅

AC ≅ CB

Midpoint

The midpoint of a segment is the point that divides the segment into two congruent segments.

Matching tic marks identify congruent segments in diagrams.

A line segment A to B has point C between them. The tick marks on A to C and on C to B indicate equal lengths of line

 

Think of the relationships between the segments AC ≅ CB so if AC=12 then CB=12

The line A to B is broken into the individual parts A to B, A to C, and C to B

also line segment AB is twice the measure of AC or CB so if CB = 7 then AC =7 and AB ≅ 2 x CB, AB= 2 × 7, or 14

 

If AC ≅ CB and AC = 8

then CB = 8 and AB = 16

A line segment A to B has point C between them. The tick marks on A to C and on C to B indicate equal lengths of line

 

Using Algebra

AC ≅ CB

2x -7 = x + 2

-x

x - 7 = 2

+ 7 + 7

x = 9

Check It!

Segment Bisector

A segment bisector is a segment, ray, line, or plane that intersects a segment at its midpoint.

The segment A to B has a line E to D that intercepts it at its midpoint

 

Indicating Congruence

If there are multiple pairs of congruent segments (which are not congruent to each other) in the same figure, use two tic marks for the second set of congruent segments, three for the third set, and so on. Notice the marks on the following parallelogram.

Parallelogram with points A, B, C, and D. Sides A to C and B to D are both marked with double dashes indicating equal length

 

Finding Midpoint

When graphing on a coordinate plane you can find the midpoint of a line segment if you know the coordinates of the endpoints. This method is summarized as the midpoint formula.

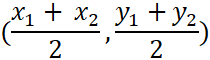
The midpoint formula. The average of the x values gives your new x value and the average of your y values gives your new y value: (half the sum of x1 and x2, half the sum of y1 and y2)

A line segment of point B (-1, 5) and point A (3, 1)

Here is a line segment on a coordinate plane with endpoints A(3,1) and B(-1,5). Using midpoint formula we can calculate the exact location a point will bisect the segment into two congruent smaller segments.

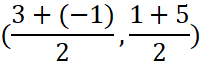
half of (3 plus -1), half of (1 plus 5)

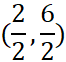
(2 over 2, 6 over 2)

(1,3)

Check It!

Find the midpoint of a line segment with endpoints (-4,3) and (8, -9)

Line segment with point C at (-4, 3) and point B at (8, -9)

Simplify the fractions. Drag the midpoint to the appropriate point on the line segment.

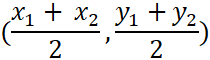
The midpoint formula. The average of the x values gives your new x value and the average of your y values gives your new y value: (half the sum of x1 and x2, half the sum of y1 and y2)

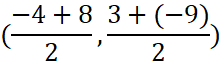
half of (-4 plus 8), half of (3 plus -9)

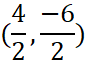
(4 over 2, -6 over 2)

(2, -3)

Previous Page