Learn
Hamiltonian and Hamilton Path
Hamilton Circuit
Do you remember what a Hamilton circuit is?
A Hamilton circuit is a circuit or cycle that includes each vertex of a graph exactly once except for the initial vertex and the final vertex, which are the same.
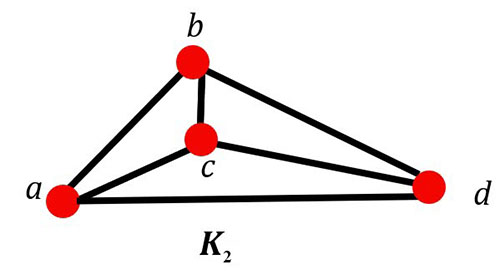
Look at the two graphs K1 and K2 below. Which one has a Hamilton circuit and which one does not?
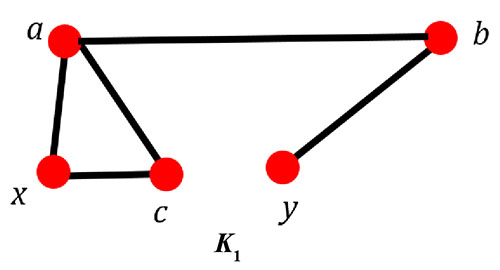
Answer: In graph K1, we can touch every vertex by following a path from (y, b, a, x, c). However, we cannot finish back at vertex y without using another vertex before we return to y.
In graph K2, we can go from (a, c, b, d, a). The Hamilton circuit is complete.
Hamiltonian
Definition: If there exists a Hamilton circuit, then the graph is Hamiltonian.
Look at the graph K3 below. This is a cube or graph with 8 vertices.
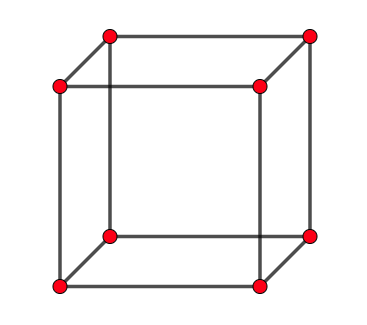
There is a Hamilton circuit from (a, b, c, d, e, f, g, h, a).
Hamilton Path
Remember a Hamilton path in a graph is a path that includes each vertex once and only once.
If you have a Hamilton circuit, like we did in graph K3 and remove the last edge, what do we have?
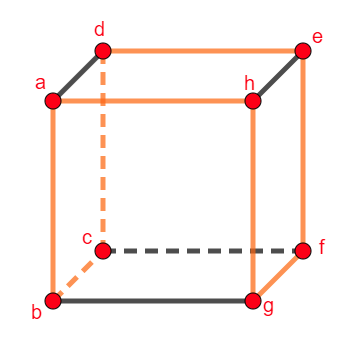
Answer: You have a Hamilton path from (a, b, c, d, e, f, g, h).
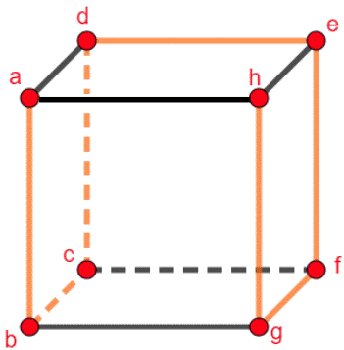
Adding Edges in a Hamilton Circuit
What happens if you add an edge to a Hamilton circuit in the graph K3?

Answer: Because the graph is Hamiltonian, adding an extra edge between two vertices results in a graph that is still Hamiltonian. In general, if you have a Hamiltonian graph and you add more edges to the graph, then you still have a Hamiltonian graph as long as you do not add any more vertices.
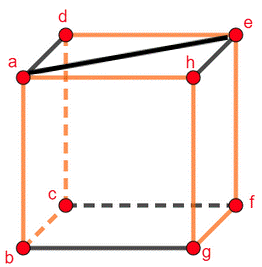
Hamiltonian Investigation
Definition: If A is a subgraph of B, then B is said to be a supergraph of A. The notation is A ⊆ B.
If graph A is Hamiltonian, then any supergraph A' (pronounced "A prime") where A' is obtained by adding new edges between non-adjacent vertices of A is also Hamiltonian.
Observation: The circuit on n vertices is Hamiltonian. We can say that An is Hamiltonian using mathematical notation.
Example #1
In this example, let A' be a complete supergraph of A. Remember, a complete graph has every vertex connected to every other vertex by an edge.
If A is Hamiltonian, then we know that the complete graph A' is also Hamiltonian. A ⊆ A'
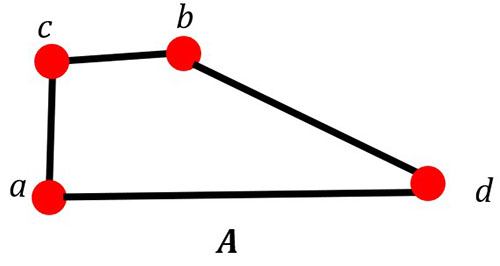
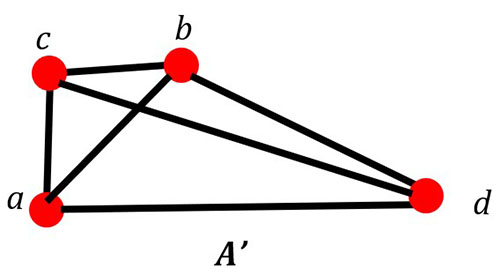
Bipartite Graphs and Hamiltonian
Hamiltonian Example
Remember If V1 has n elements and V2 has m elements, then the resulting bipartite graph is denoted Kn, m.
Show that Kn, m is Hamiltonian if and only if m = n and each has at least 2 vertices in each of the partite sets.
We are not going to prove this, but we want to explore a few different examples.
Example #2
Let Kn, m have a bipartition V1 and V2 where V1= n vertices and V2 = m vertices.
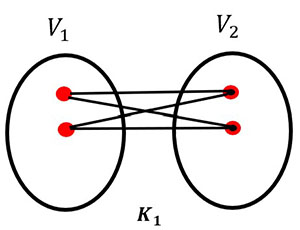
The graphs K1 and K2 have a bipartite and both parts of the graph have the same vertices.
How many edges are there in each graph?
Answer: K1 = 4 edges and K2 = 6 edges
Your Turn #1 Hamiltonian
Determine if the bipartite graphs below have an even or odd number of edges.
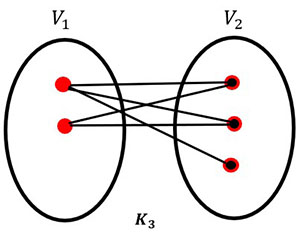
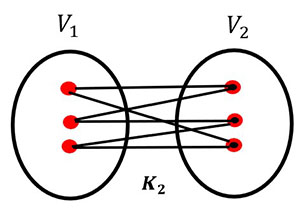
How many edges does K3 have?
Answer: K3 has 5 edges (odd), so this is a Hamilton path
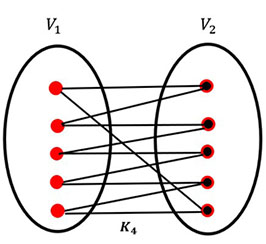
How many edges does K4 have?
Answer: K4 has 10 edges (even), so this is a Hamiltonian.
Is This Hamiltonian?
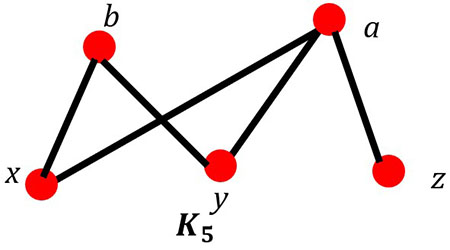
Look at the graph K5 above. Does it contain a Hamilton path? If it does, what is the path?
Possible answers are: (z, a, y, b, x), (x, b, y, a, z), or (y, b, x, a, z)
Is K5 Hamiltonian?
Hint: Try starting at all 5 vertices.
| Vertices | Possible paths | Comments |
|---|---|---|
| a | (a, x, b, y, a, z, a) or (a, y, b, x, a, z, a) | Notice how in both paths you have to go through a 3 times. |
| b | (b, x, a, y, a, z, a, y, b) or (b, y, a, z, a, y, b) | Notice how you cannot get back to b without going through other vertices more than once. |
| x | (x, b, y, a, z, a, x) or (x, a, z, z, y, b, x) | Notice how you cannot get back to x without going through other vertices more than once. |
| y | (y, b, x, a, z, a, y) or (y, a, z, a, x, b, y) | Notice how you cannot get back to y without going through other vertices more than once. |
| z | (z, a, y, b, x, a, z) or (z, a, x, b, y, a, z) | Notice how you cannot get back to x without going through other vertices more than once. |
Answer: No, K5 is not Hamiltonian.
Example #3 Connected Graph without Hamilton Path
Which connected graphs do not have Hamilton paths?
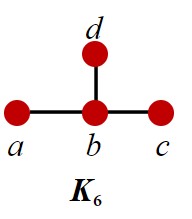
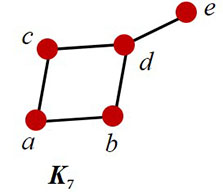
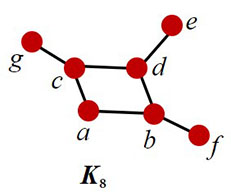
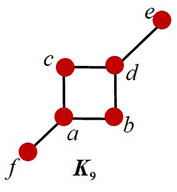
- K6
- K7
- K8
- K9
Answer(s): K6, K8, and K9
Hamilton Path and Hamilton Circuit
Look at the graph K10. Can a Hamilton path always be used to form a Hamilton circuit?
Explain.
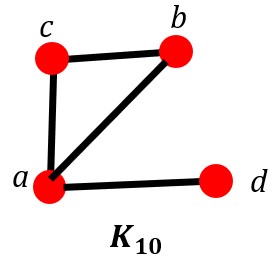
Answer: No, it can't be used to form a Hamilton circuit. You can travel from (b, c, a, d) which is a Hamilton path, but you cannot get back to b without crossing back over one of the same vertices. Even going from (c, b, a, d) is a Hamilton path, but you cannot get back to c without crossing a again.
Trees
Tree Graphs
What is the relationship between the vertices of a tree graph and the edges?
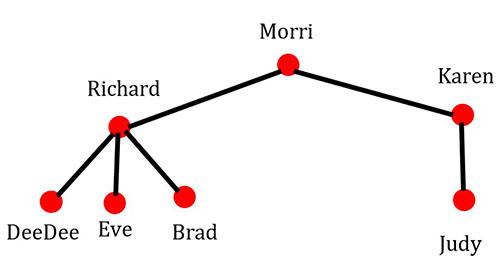
Example #4
In K11 below, you see that there are 7 vertices and 6 edges.
Example #5
In K12 below, you see that there are 8 vertices and 7 edges.
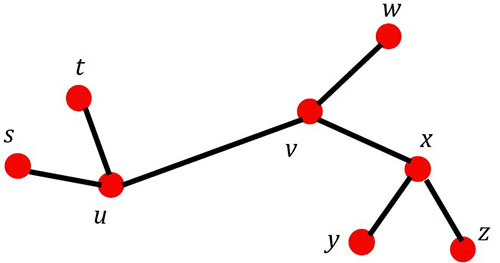
From the examples, it looks like if the number of vertices is n, then the number of edges is n − 1 or 1 less than the number of vertices.
Tree Graph Properties
In every tree, the number of edges is equal to the number of vertices − 1.
Written mathematically:
Theorem: In every tree T with <v, e>, e = v − 1
Remember proof by induction?
- Show true for e = 0. Since there are no edges, then we have 1 vertex. 0 = 1 − 1.
- Assume e ≥ 1 . There is at least 1 edge. Then we know there is at least 1 vertex v ∈ T.
- So T' = T − v. What does this mean?
Example #6
Tree T has 5 vertices and 4 edges. If you take 1 vertex away you still have a tree T' with 4 vertices and 3 edges.
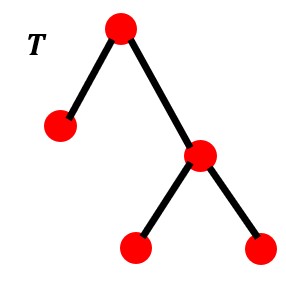
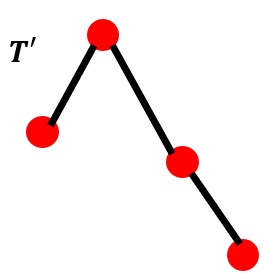
We have a smaller tree in T'. What do we know about the edges in T' ? We know that e' = e − 1 because we removed 1 vertex, so one edge will be removed. So, the number of vertices v' = v − 1.
Then we have e'= v'− 1 because the induction hypothesis says:
- e = v −1
- e' + 1 = v' + 1 − 1
- e' + 1 = v'
- e' = v' − 1
So, we have proved that e = v − 1.
Example #7 Tree Graph Property
Let T1 = (v1, e1) and T2 = (v2, e2) be two trees with e1 = 17 and v2 = 2v1
Find v1, v2, e2.
e = v − 1
e1 = 17 = v1 − 1
v1 = 17 + 1 = 18
v2 = 2(v1) = 2(18) = 36
e1 = v2 − 1 = 36 − 1 = 35
So, we got:
- v1 = 18,
- v2 = 36, and
- e2 = 35.
Your Turn #2 Tree Graph Property
Let T1 = (v1, e1) and T2 = (v2, e2) be two trees with e1 = 20 and v2 = 3v1
Find v1, v2, e2.
e = v − 1
e1 = 20 = v1 − 1
v1 = 20 + 1 = 21
v2 = 3(v1) = 3(21) = 63
e1 = v2 − 1 = 63 − 1 = 62
So, we got:
- v1 = 21,
- v2 = 63, and
- e2 = 62.
Your Turn #3
Let T1 = (v1, e1) and T2 = (v2, e2) be two trees with e1 = 15 and v2 = 2 + 4v1
Find v1, v2, e2.
e = v − 1
e1 = 15 = v1 − 1
v1 = 15 + 1 = 16
v2 = 2 + 4(v1) = 2 + 4(16)
= 2 + 64 = 66
e1 = v2 − 1 = 66 − 1 = 65
So, we got:
- v1 = 16,
- v2 = 66, and
- e2 = 65.
Example #8 Tree or not Tree
Give a graph G = (v, e) where v = e + 1, but G is not a tree. These two graphs below are examples that have 5 vertices and 4 edges and are not trees.
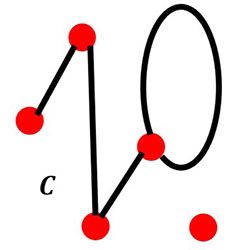
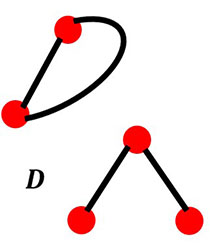
Your Turn #4
Give a graph G = (v, e) where v = e + 1, but G is not a tree. The graphs below are examples of how many vertices and how many edges?
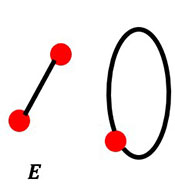

These two graphs have:
- 3 vertices, and
- 2 edges.