Learn
Euler Paths and Circuits
Leonhard Euler
Leonhard Euler was an extraordinary mathematician of the eighteenth century who did groundbreaking work in many different mathematical fields. He is understood as the father of graph theory.

Euler Path
We have already looked at simple paths in the previous lesson. A simple path is a path in which no edge is repeated twice. In the figure below, we can travel from (x, a, b, y) without using an edge more than once.
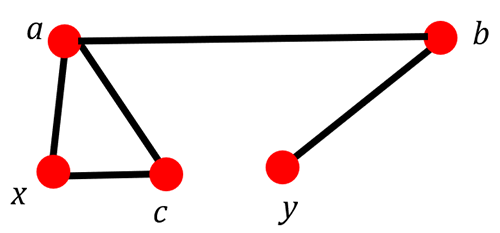
An Euler path in a graph is a simple path that includes each edge of the graph.
The figure below is an Euler path. You can travel from (a, b, c, d, e, a, e) and only cross the path once.
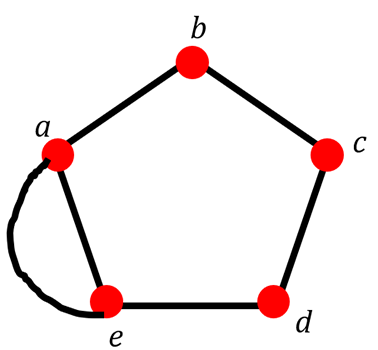
Your Turn #1 Euler Path
Find a path for using every edge in the figure K1.
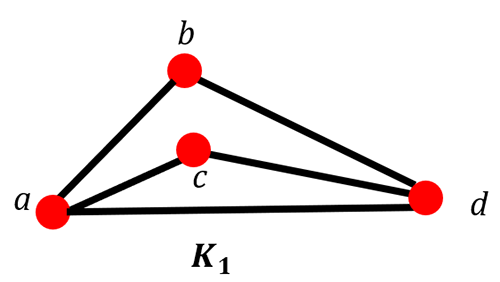
Answer: (a, b, d, a, c, d)
Euler Circuits
An Euler circuit is a circuit that is an Euler path. This means that you start at the same vertex and include every edge, but you return to the same vertex.
In the graph K2 below, identify the Euler circuit. See how you start at q and end with q only using each edge once.
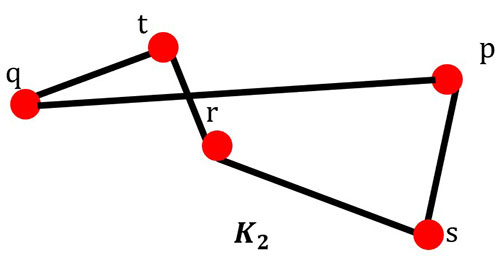
The Euler circuit for graph K2 is (q, t, r, s, p, q).
Your Turn #2 Euler Circuits
In the graph K3 , identify the Euler circuit.
Hint: Start at vertex a or e.
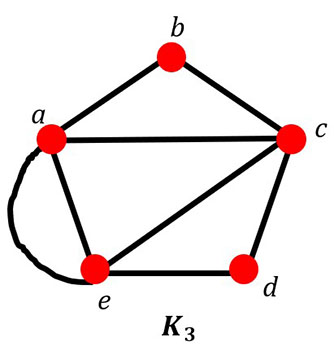
Possible answers: (a, b, c, d, e, a, c, e, a) or (a, c, e, d, c, b, a, e, a)
Hamilton Paths and Circuits
Hamilton Paths
Lord William Rowan Hamilton (1805-1863) was the most noted Irish scientist and mathematician of his century.
A Hamilton path in a graph is a path that includes each vertex once and only once.
Example #1
In the K1 graph below, the purple line is an example of a Hamilton path.
The path goes from (x, b, y, a, z).
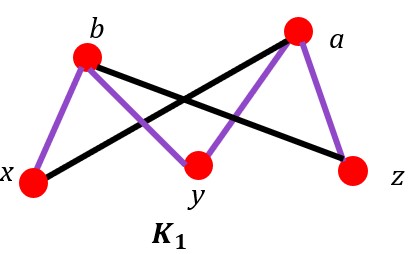
Example #2
In the K2 graph, the purple line is an example of a Hamilton path.
The path goes from (a, b, e, d, c).
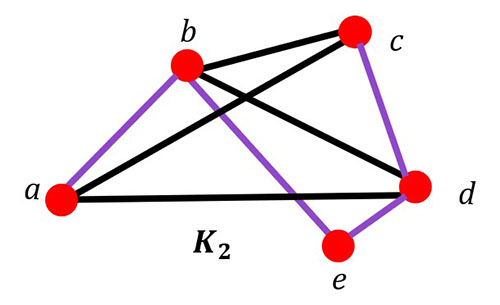
Example #3
There can be more than one Hamilton path in the same graph.
In the K3 graph, the purple line is an example of a Hamilton path.
The path goes from (a, b, c, d, e).
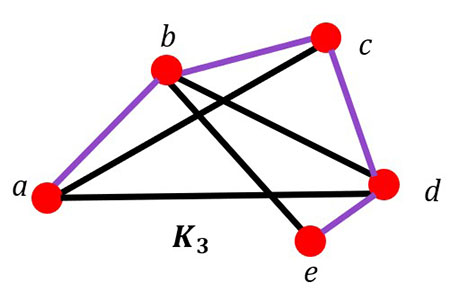
Your Turn #3 Name the Hamilton Path
Identify at least 2 different Hamilton paths in the graph K4.
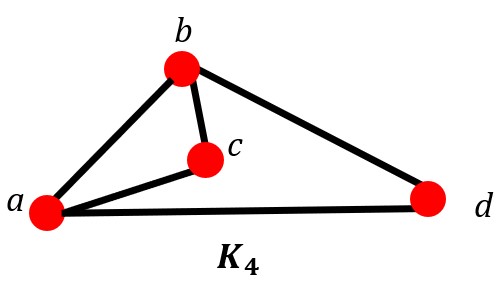
Possible answers: (a, c, b, d), (c, a, b, d), (d, b, c, a), (d, b, a, c), (d, a, c, b), or (d, a, b, c)
Hamilton Circuits
A Hamilton circuit is a circuit that includes each vertex of a graph exactly once except for the initial vertex and the final vertex, which are the same.
Example #4: In the K5 graph, the purple line is an example of a Hamilton circuit.
The path goes from (a, b, d, c, a) or (a, c, d, b, a).
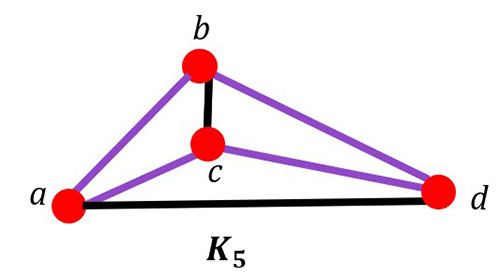
Your Turn #4 Find a Hamilton Circuit
There are two Hamilton circuits that start from vertex a in the graph K6.
Identify the path of both circuits.
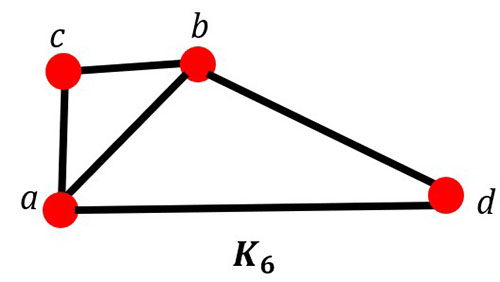
Answers: (a, c, b, d, a) and (a, d, b, c, a)
Euler and Hamilton
Example #5 Euler and Hamilton
Identify any
- Euler paths,
- Euler circuits,
- Hamilton paths,
- Hamilton circuits
if possible in graph K7.
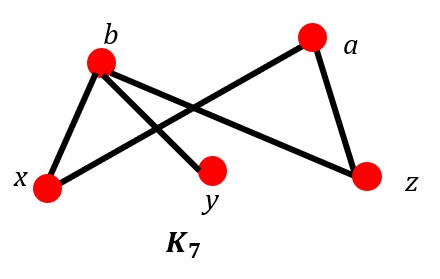
Solution:
- Euler path: (y, b, z, a, z, b)
- Euler circuit: There is not an Euler circuit.
- Hamilton path: (y, b, x, a, z)
- Hamilton circuit: There is not a Hamilton circuit.
Your Turn #5
Identify any
- Euler paths,
- Euler circuits,
- Hamilton paths,
- Hamilton circuits
if possible in graph K8.
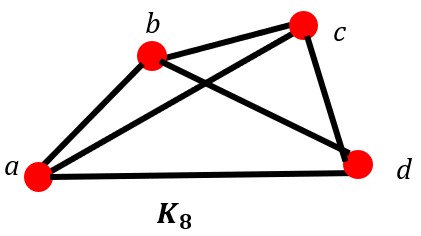
Answers:
- Euler path: There is not an Euler path.
- Euler circuit: There is not an Euler circuit.
- Hamilton path:(a, b, c, d), (a, d, c, b), (a, c, d, b) are possible answers.
- Hamilton circuit: (a, b, c, d, a), (a, c, b, d, a), (a, d, b, c, a) are possible answers.