- Introduction
Learn- Try It
- Task
Learn
Read the following chapters in The Practice of Statistics
- 2003: pgs 481-486
- 2012: pgs 346-348
It is now time to look at the mean and variance of discrete random variables. Earlier in the course, the mean and standard deviation were used to describe a frequency distribution. Similarly, the mean and standard deviation are used to describe a probability distribution.
Expected Value (Mean) of a Probability Distribution
An emergency room needs to be prepared for an expected number of patients with heart problems per day. A restaurant wants to serve all customers and needs to know how many hamburgers are expected to be sold per say. As a safety issue, a city manager wants to know how many fires can be expected in the next year and if there is a need for another fire station. Many situations require an expected value. The expected value is the average (mean) of the probability distribution. It is denoted by an "E" and is defined by the formula
EXPECTED VALUE (MEAN)
E = 
(x · P(x))
where: is the Greek letter sigma, meaning add.
x is the random variable.
P(x) is the random variable's corresponding probability.
Consider the 500 speeders from the problem below. The probability distribution is:
Prior Speeding Tickets
x |
Frequency |
P(x) |
0 |
120 |
|
1 |
200 |
|
2 |
70 |
|
3 |
60 |
|
4 |
40 |
|
5 |
10 |
|
Totals |
500 |
|
= 0.24
= 0.40
= 0.14
= 0.12
= 0.08
= 0.02
= 1.00To find the average number of speeding tickets for the people in traffic court, add a new column, "x • P(x)". For each random variable, x, find the product of "x" and its corresponding probability, "P(x)." Lastly, find the sum of this column.
Prior Speeding Tickets
x |
Frequency |
P(x) |
x • P(x) |
0 |
120 |
|
0.00 |
1 |
200 |
|
0.40 |
2 |
70 |
|
0.28 |
3 |
60 |
|
0.36 |
4 |
40 |
|
0.32 |
5 |
10 |
|
0.10 |
Totals |
500 |
|
1.46 |
The average number of speeding tickets for the people in this traffic court is approximately 1.46 tickets. Most people in this court have an average between one and two speeding tickets.
Variance,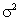 
, of a Probability Distribution
where means add
x is the random variable
is the mean of the probability distribution
Standard Deviation,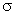 
, of a Probability Distribution
where means add
x is the random variable
is the mean of the probability distribution
To calculate the standard deviation of a probability distribution, one more column, x2P(x), needs to be added to the table used to calculate the mean. Find the standard deviation for the speeding ticket problem above.
Prior Speeding Tickets
x |
Frequency |
P(x) |
x · P(x) |
x2 P(x) |
0 |
120 |
|
0.00 |
0.00 |
1 |
200 |
|
0.40 |
0.40 |
2 |
70 |
|
0.28 |
0.56 |
3 |
60 |
|
0.36 |
1.08 |
4 |
40 |
|
0.32 |
1.28 |
5 |
10 |
|
0.10 |
0.50 |
Totals |
500 |
|
1.46 |
3.82 |
= ≈1.30 (1.462 = 2.1316) The probability distribution's standard deviation is approximately 1.30 speeding tickets.
Find the average, money won/loss for the following raffle:
Solution:
Step 1: Understand and Picture the Problem.
Make a probability distribution table to calculate the expected value. This value
is also known as the average.
Step 2: Develop a Plan.
a. Make a table labeling one column "Event" (How much money can be won).
b. Label another column "x", this is the random variable, it is the winnings
MINUS the cost of the ticket.
c. Label the next column "Frequency", this is the number of winners for each
prize.
d. Label the next column "P(x)". This is the probability for each event.
e. Label the last "x * P(x)". This column will be used to calculate the expected
value (Average).
f.. Calculate the product "x * P(x)" by multiplying the random variable, "x", by its
corresponding probability, "P(x)".
g. Find the sum of this column.
Step 3: Execute the Plan.
Saint Mary's Raffle
| Event | x |
Frequency |
P(x) |
x * P(x) |
| Win $25,000 | $24,900 | 1 | 1 / 1,200 | $24,900 / 1,200 |
| Win $10,000 | $9,900 |
1 | 1 / 1,200 |
$9,900 / 1,200 |
| Win $5,000 | $4,900 |
1 | 1 / 1,200 |
$4,900 / 1,200 |
| Win Big Screen TV (worth $2,000) | $1,900 |
1 | 1 / 1,200 |
$1,900 / 1,200 |
| Win $1,000 | $900 |
9 | 9 / 1,200 |
$8,100 / 1,200 |
| Win $500 | $400 |
7 | 7 / 1,200 |
$2,800 / 1,200 |
| Win $150 | $50 |
40 | 40 / 1,200 |
$2,000 / 1,200 |
| Lose, (Win $0) | -$100 | 1,140 | 1,140 / 1,200 | -$114,000 / 1,200 |
Totals |
1,200 |
1,200/1,200 |
-$59,500 / 1,200 |
The average money lost by a ticket buyer in the raffle is -$59,500 / 1,200.
This means that the charity made $59,500 / 1,200 per ticket sold. Since there were 1,200 ticket sold, the charity made a profit of 
Step 4: Check Your Work.
a. Check your numbers and calculations.
b. Was the question answered?
c. At $100 a ticket, selling 1,200 tickets produces a Revenue of
$100(1,200) = $120,000.The Costs of the prizes are:
$25,000 + $10,000 + $5,000 + $2,000 + $9,000 + $3,500 + $6,000 = $60,500Profit = Revenue -Cost = $120,000 -$60,500 = $59,500.
This matches the profit calculated using the expected value.
Use the following websites if you need additional help.
